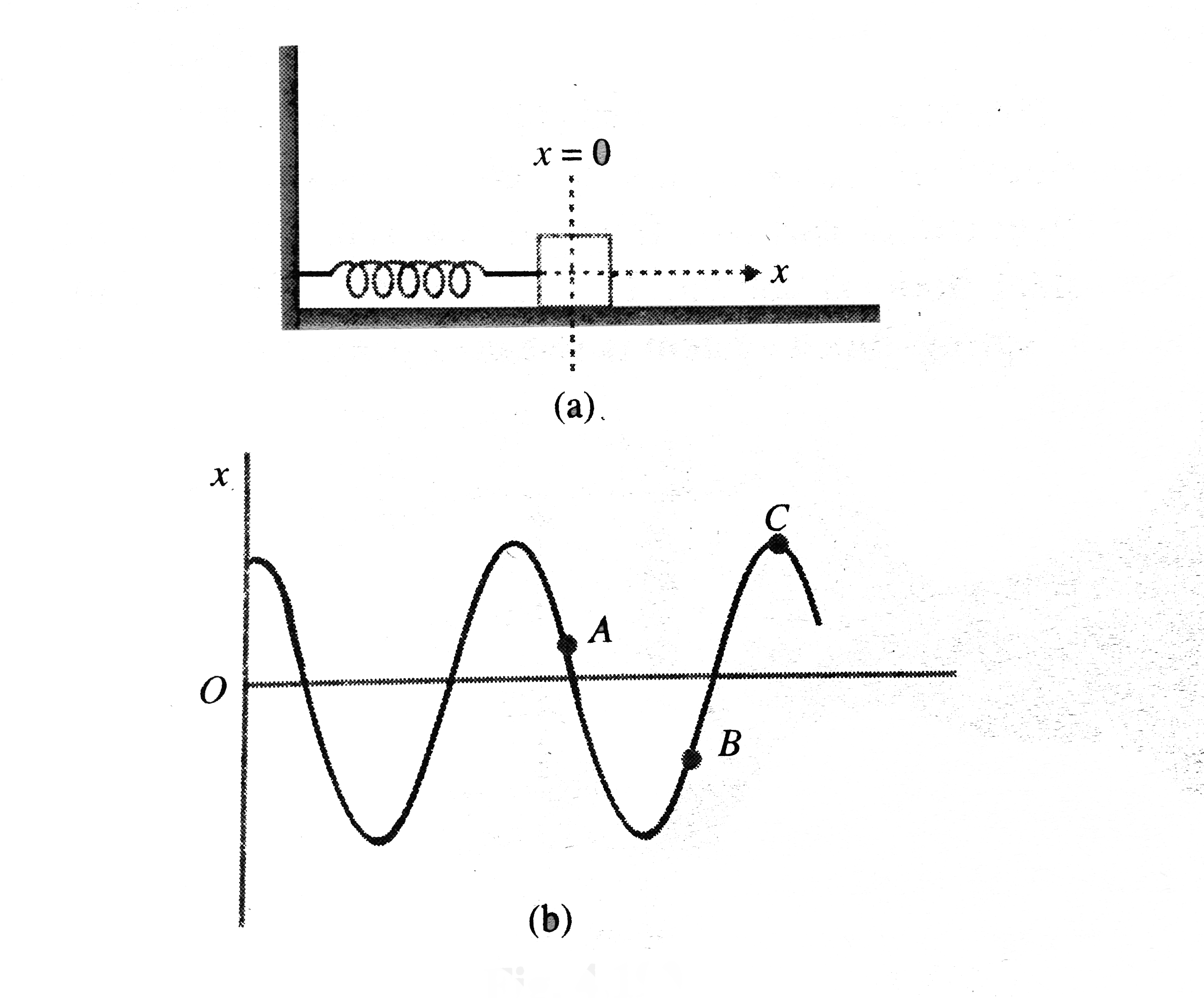
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Velocity of the block as a function of time can be expressed as
v=−sin48(16tπ2)cms
v=−48sin(16tπ3)cms
v=−56sin(16tπ4)cms
v=−56(16tπ6)cms
The correct Answer is:D
Differentiating previous result
v=−31√3sin(16t+π6)cms
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer10videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type2videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning6videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
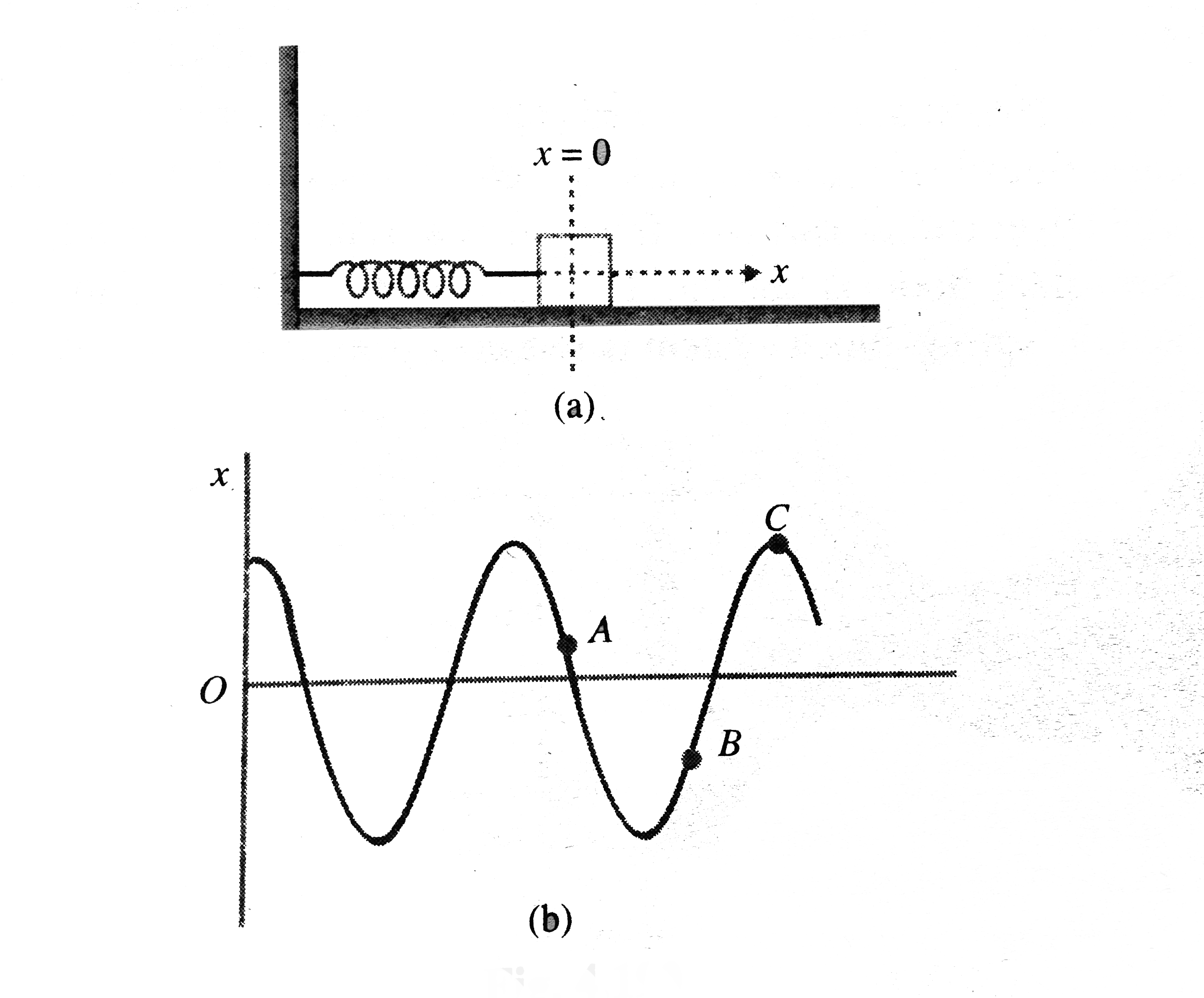
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Q. When the block is at position B on the graph its.View SolutionA 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_050_Q01.png)
When the block is at position A on the graph, itsView Solution
Knowledge Check
- Question 1 - Select One
A 10 kg mass is connected at one end of a massless spring with force constant k = 1000 N/m, keeping other end fixed in a horizontal plane as shown in the fig. 15.6
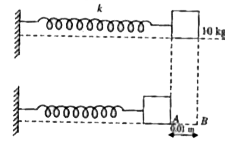If the sytem is displaced by 0.01 m from its equilibrium position A to a point B, then the acceleration of the system is A10ms−2B1ms−2C−1ms−2D−10ms−2
A 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_052_Q01.png)
Let us now make a slight change to the initial conditions. At t=0, let the block be released from the same position with an initial velocity v1=64cm/s. Position of the block as a function of time can be expressed asView SolutionA small block is connected to one end of a massless spring of un-stretched length 4.9 m. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by 0.2 m and released from rest at t = 0. It then executes simple harmonic motion with angular frequency ω=π3rad/s . Simultaneously at t = 0, a small pebble is projected with speed ν from point P at an angle of 45∘ as shown in the figure. Point P is at a horizontal distance of 10 m from O. If the pebble hits the block at t = 1s, the value of ν is (take g = 10 m/s2 )
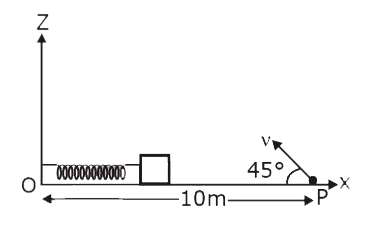
View SolutionA small block is connected to one end of a massless spring of un - stretched length 4.9m. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by 0.2m and released from rest at t=0. It then executes simple harmonic motion with angular frequency (ω)=(π/3)rad/s. Simultaneously at t=0, a small pebble is projected with speed (v) from point (P) at an angle of 45∘ as shown in the figure. Point (P) is at a horizontal distance of 10momO. If the pebble hits the block at t=1s, the value of (v) is (takeg=10m/s2).
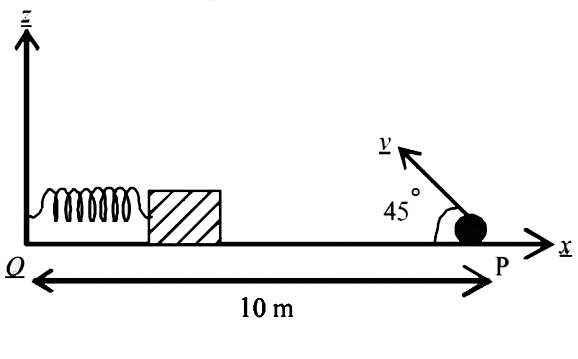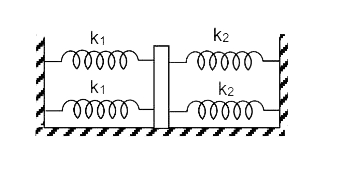
.View SolutionA block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.
View SolutionA 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)
View Solution