Let f(x) =x+logex−xlogex,x(0,∞). Column 1 contains information about zeros of f′(x)f′(x)andfx. Column 2 contains information about the limiting behaviour of f′(x)f′(x)andfx at infinity. Column 2 contains information about the increasing/decreasing nature of f(x)andf′(x). Column I, Column 2, Column 3 I, f(x)=0forsomex(l,e2) , (i), (lim)x→∞f′(x)=0 , (P), f is increasing in (0,1) II, f'(x)=0forsomex(l,e) , (ii), (lim)x→∞fx=−∞ , (Q), f is decreasing in (e,e2) III, f'(x)=0forsomex(0,1) , , (lim)x→∞f′(x)=−∞ , (R), f is increasing in (0,1) IV, f''(x)=0forsomex(1,e) , , (lim)x→∞f′^'(x)=0 , (S), f is decreasing in (e,e2 ) Which of the following options is the only CORRECT combination? (I) (ii) (P) (b) (IV) (iv) (S) (III) (iii) (R) (d) (II) (ii) (Q) Which of the following option is the only incorrect combination? (III) (i) (R) (b) (I) (iii) (P) (II) (iii) (P) (d) (II) (iv) (Q) Which of the following options is the only CORRECT combination? (I) (ii) (R) (b) (II) (iii) (S) (III) (iv) (P) (d) (IV) (i) (S)
Step by step video & image solution for Let f(x) =x+log_ex-xlog_ex ,x(0,oo)dot Column 1 contains information about zeros of f^(prime)(x)f^(prime)(x)a n df^(x)dot Column 2 contains information about the limiting behaviour of f^(prime)(x)f^(prime)(x)a n df^(x) at infinity. Column 2 contains information about the increasing/decreasing nature of f(x)a n df^(prime)(x)dot Column I, Column 2, Column 3 I, f(x)=0forsom ex(l , e^2) , (i), ("lim")_("x"vecoo"")f^(prime)(x)=0 , (P), f is increasing in (0,1) II, f'(x)=0forsom ex(l , e) , (ii), ("lim")_("x"vecoo"")f^(x)=-oo , (Q), f is decreasing in (e ,e^2) III, f'(x)=0forsom ex(0,1) , , ("lim")_("x"vecoo"")f^(prime)(x)=-oo , (R), f is increasing in (0,1) IV, f^(' '(x))=0forsom ex(1, e) , , ("lim")_("x"vecoo"")f^prime^'(x)=0 , (S), f is decreasing in (e , e^2 ) Which of the following options is the only CORRECT combination? (I) (ii) (P) (b) (IV) (iv) (S) (III) (iii) (R) (d) (II) (ii) (Q) Which of the following option is the only incorrect combination? (III) (i) (R) (b) (I) (iii) (P) (II) (iii) (P) (d) (II) (iv) (Q) Which of the following options is the only CORRECT combination? (I) (ii) (R) (b) (II) (iii) (S) (III) (iv) (P) (d) (IV) (i) (S) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Let the function f satisfies f(x)⋅f′(−x)=f(−x)⋅f′(x) foe all x and f(0)=3 The value of f(x).f′(−x)=f(−x).f′(x) for all x, is
View SolutionIf f(x)=logx(logex) then f'(e)=________
View SolutionIf f:R→R is a differentiable function such that f′(x)>2f(x)forallxRandf(0)=1,then: f(x) is decreasing in (0,∞) f′(x)<e2x∈(0,∞) f(x)="" is="" increasing="" in="" (0,∞)="" f(x)=>e2x∈(0,∞)>
View SolutionA differentiable function satisfies f′(x)=f(x)+2ex with initial conditions f(0)=0. The area enclosed between f(x) and the x -axis is.
View SolutionIf f′x=g(x)(x−a)2,whereg(a)≠0,andg is continuous at x=a, then f is increasing in the neighbourhood of a if g(a)>0 f is increasing in the neighbourhood of a if g(a)<0 f is decreasing in the neighbourhood of a if g(a)>0 f is decreasing in the neighbourhood of a if g(a)<0
View SolutionLet f(x+y)=f(x)f(y) for all x and y . Suppose f(5)=2 and f′(0)=3 , find f′(5) .
View SolutionThe graph of y = f(x) is as shown in the following figure.
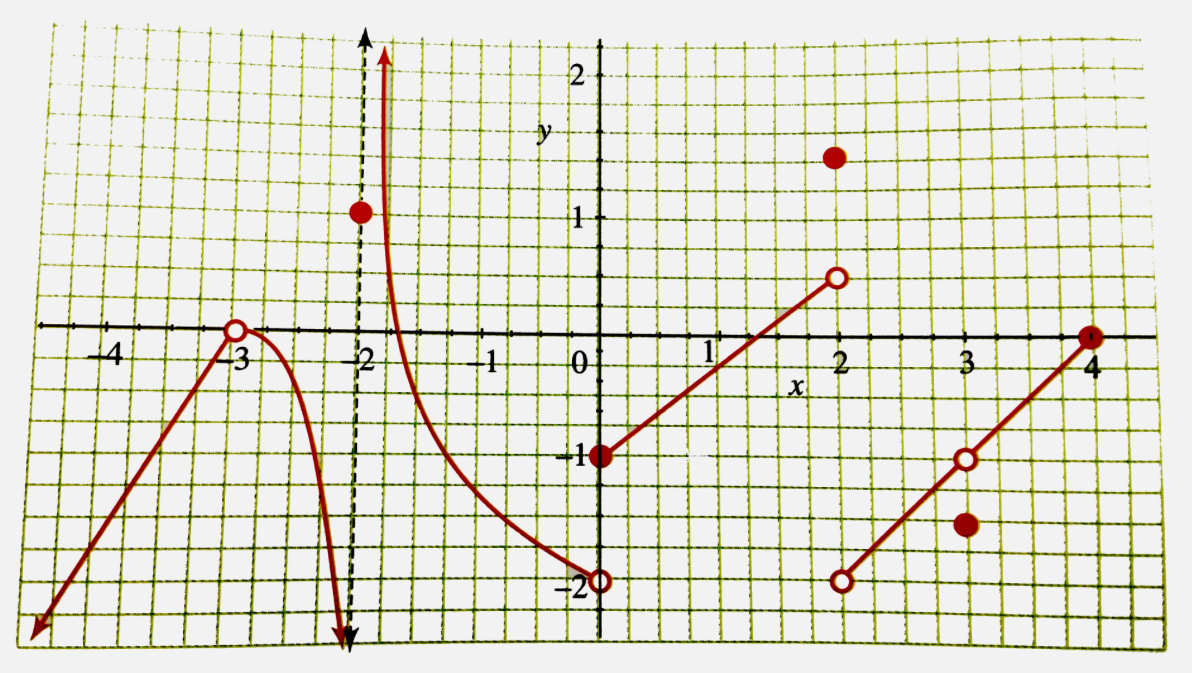
Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View SolutionIf f(x)=|x−a|ϕ(x), where ϕ(x) is continuous function, then (a) f′(a+)=ϕ(a) (b) f′(a−)=−ϕ(a) (c) f′(a+)=f′(a−) (d) none of these
View SolutionIf y=f(x) satisfies the differential equation (1+x2)f′(x)=x(1-f(x)), f(0)=4/3,thenf∈dthevalueoff(sqrt8)+8/9
View SolutionIf [.] is the greatest integer function and f(x)=[tan2x], then (a)(lim)x→0f(x) does not exist (b)f(x) is continuous at x=0 (c)f(x) is not differentiable at x=0 (d)f′(0)=1
View Solution
