Total number of integral values of 'a' so that x2−(a+1)x+a−1=0 has roots, is equal to :
2
1
4
none of these
The correct Answer is:B
x2−ax−x+a−1=0
x2−ax−x+a=1
(x−a)↓integer(x−1)↓integer=1↓integer x,aεintegeronly possible if
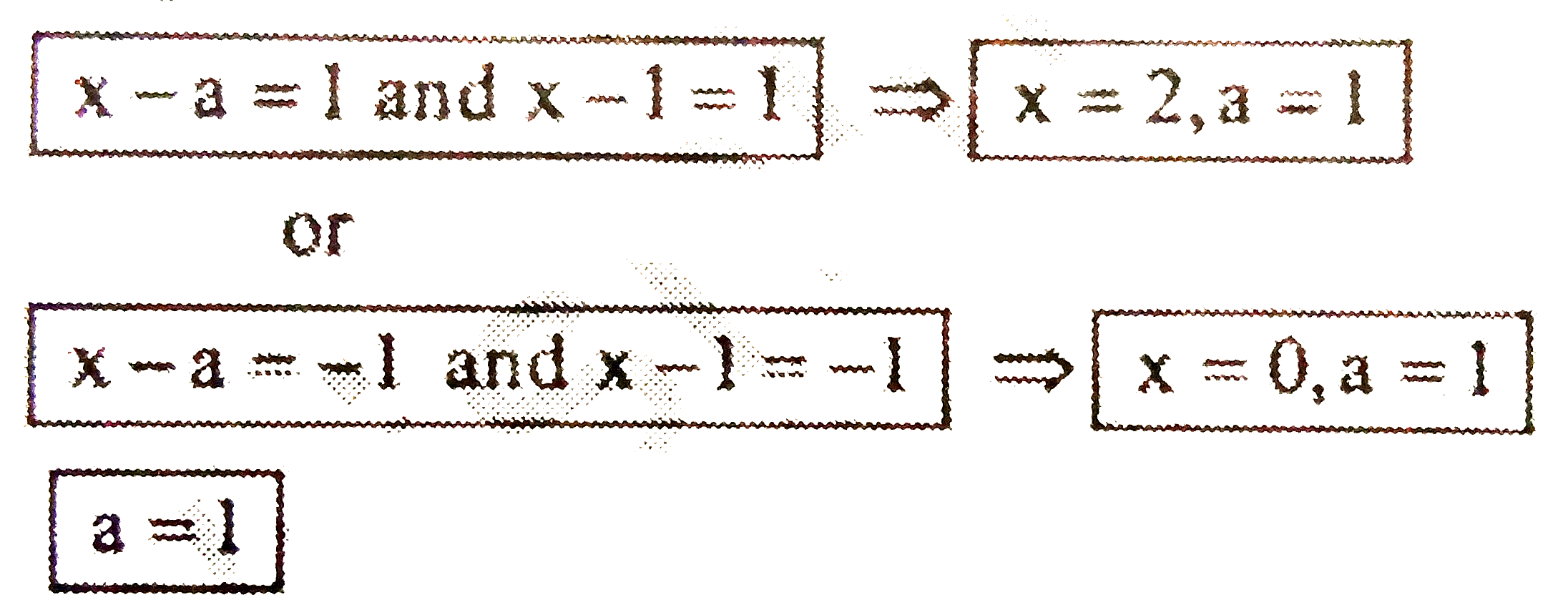
is only single a for which it is possible
Topper's Solved these Questions
Similar Questions
Knowledge Check
The number of integral values of a for which x2−(a−1)x+3=0 has both roots positive and x2+3x+6−a=0 has both roots negative is
A0B1C2Dinfinite
Match the following :
Column I Column II (A) The total number or real solutions of the equation(x2−7x+1)(x2−11x+30)=1is(p)2(B) Total number of values of a so that x2−x−a=0 has distinct integral roots, where a∈and6≥a≥100 is equal to (q)4(C) The least value of n such that (n−2)x2+8x+n+4>0∀x∈R where n∈Nis(r)5(D) Total number of integral values of a such that x2+ax+a+1=0 has integral roots is equal to (t)8(t)9
View SolutionNumber of integral values of a for which the equation x2−(a+1)x+a−1=0 , has integral roots, is equal to -
View SolutionNumber of integral values of 'a' for which (a−1)x2+(a−1)x+1≥0∀x∈R ,is ?
View SolutionLet f(x)=∫x0((a−1)(t2+t+1)2−(a+1)(t4+t2+1)) dt. Then the total numbr of integral values of 'a' for which f'(x)=0 has no rel roots is
View SolutionLet f(x)=∫x0((a−1)(t2+t+1)2−(a+1)(t4+t2+1))dt then find the total number of integral value of a for which f'(x)=0 has no real root
View SolutionFind the number of integral values of 'a' for which ax2−(3a+2)x+2(a+1)<0,a≠0 holds exactly four integral value of x.
View SolutionFind the number of integral values of a so that the inequation x2−2(a+1)x+3(a−3)(a+1)<0 is satisfied by atleast one x∈R+,
View Solution
