If cos−1(cosx)=√1sin2x∀xε(0,2π), then no. of solution =
A
2
B
4
C
3
D
5
Video Solution
Text Solution
The correct Answer is:A
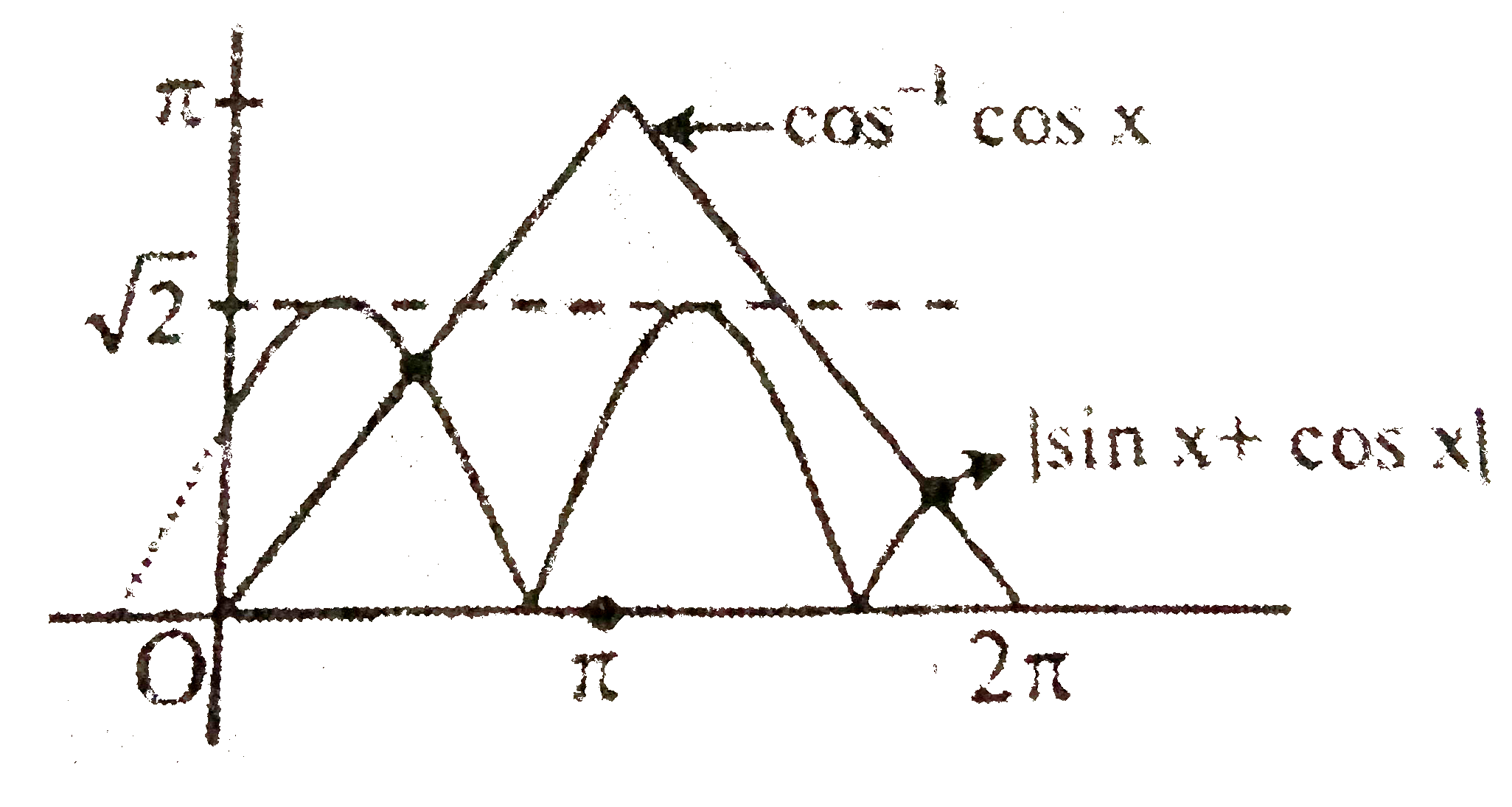
√sin2x=|sinx+cosx|
=√2∣∣∣sin(x+π4)∣∣∣
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
∫cos2x(e−x+cosx)√1+sin2xdx,x∈(0,π2) is equal to
Aloge|1+exsinx|+cBloge|ex+cosx|+cCloge|1+excosx|−x+cDloge|1+excosx|+c√cos2x+√1+sin2x=2√sinx+cosx if
Asinx+cosx=1Bx=2nπCx=nπ+π/4Dsinx−cosx=0If √1+cosx+√1−cosx√1+cosx−√1−cosx=cot(a+x2) and x∈(π,2π) then 'a' is equal to :
Aπ4Bπ2Cπ3DNone of these
Number of solutions of the equation cosec−1(cosecx)=sinx. in [−2π,2π] is 'a' and number of solutions of cosec−1(cosecx)=√sinx in this interval is 'b' then √a+b is
View SolutionIf x∈[0,2π] for which 2cosx≤∣∣√1+sin2x−√1−sin2x∣∣≤√2 has solution set x∈[λπ4,μπ4] then value of λ+μ is
View SolutionIf 2cosx(4sin(π4+x)sin(π4−x)−1)=1 then for x∈[0,π] then the number of solution s is n ,and the sum of solutions is s then find the value of (n,s)
View SolutionConsider the function f(x)=√1+cosx+√1−cosx√1+cosx−√1−cosx then
Q. If x∈(π,2π) then f(x) is
View SolutionThe total number of solutions of cosx=√1−sin2x in [0,2π] is equal to
View Solution
