The correct curve between fringe width β and distance between the slits (d) is figure is -
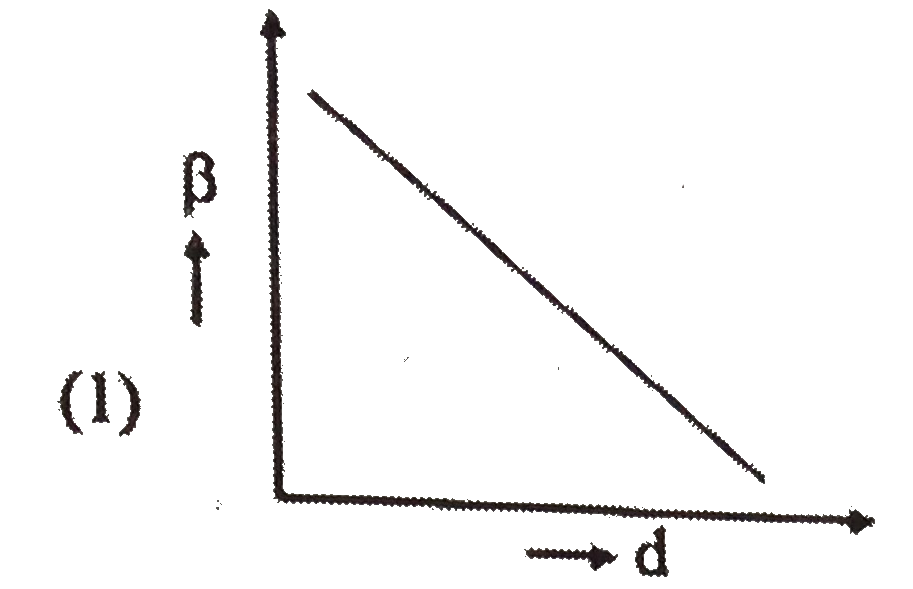
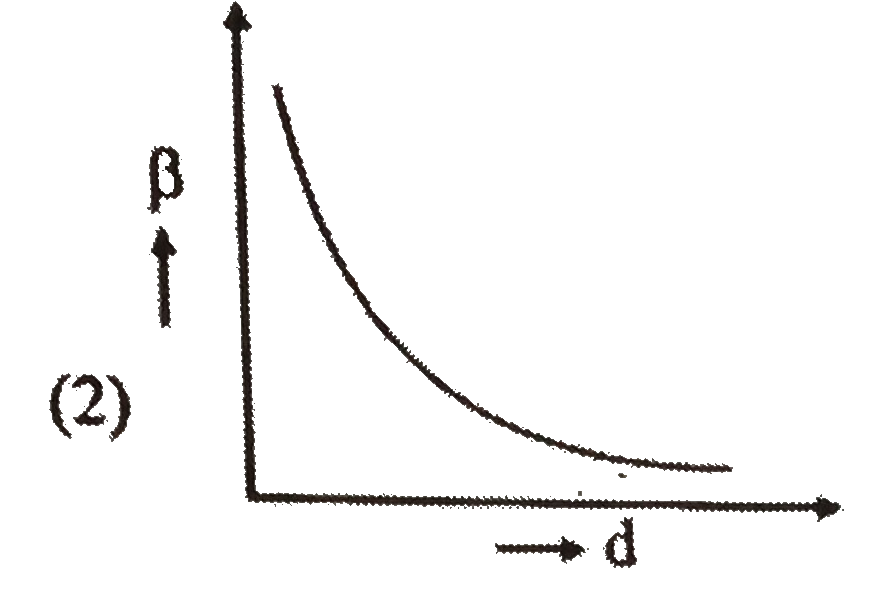
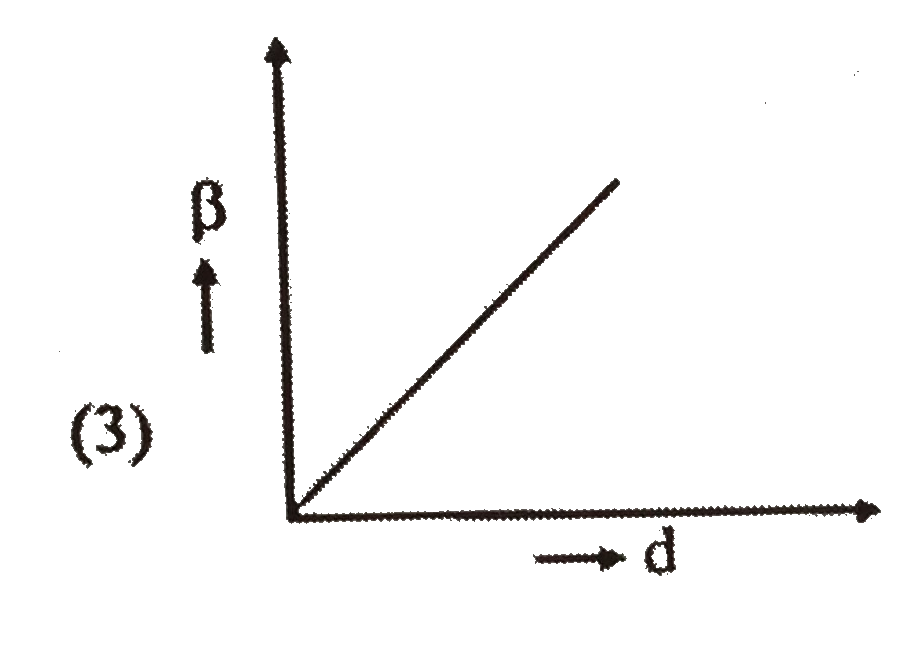

The correct Answer is:B
To solve the question regarding the relationship between fringe width (β) and the distance between the slits (d), we can follow these steps:
1. Understand the Concept of Fringe Width:
The fringe width (β) in a double-slit experiment is defined as the distance between two consecutive bright or dark fringes on the screen. The formula for fringe width is given by:
β=dλD
where:
- β = fringe width
- d = distance between the slits
- λ = wavelength of the light used
- D = distance from the slits to the screen
2. Identify the Relationship:
From the formula, we can see that fringe width (β) is directly proportional to the distance between the slits (d) and the wavelength (λ), and inversely proportional to the distance from the slits to the screen (D):
β∝d
This means that if the distance between the slits (d) increases, the fringe width (β) also increases.
3. Analyze the Graph:
Since β is directly proportional to d, if we were to plot a graph of β against d, we would expect a linear relationship. As d increases, β increases, which means the graph should slope upwards.
4. Determine the Correct Option:
Given the options in the question, we need to identify which graph represents this direct relationship. The correct graph should show an increasing trend as the distance between the slits (d) increases.
5. Conclusion:
After analyzing the options, the correct answer is the graph that shows an increasing curve between fringe width (β) and distance between the slits (d). This corresponds to the second option provided.
The fringe width (β) in a double-slit experiment is defined as the distance between two consecutive bright or dark fringes on the screen. The formula for fringe width is given by:
β=dλD
where:
- β = fringe width
- d = distance between the slits
- λ = wavelength of the light used
- D = distance from the slits to the screen
From the formula, we can see that fringe width (β) is directly proportional to the distance between the slits (d) and the wavelength (λ), and inversely proportional to the distance from the slits to the screen (D):
β∝d
This means that if the distance between the slits (d) increases, the fringe width (β) also increases.
Since β is directly proportional to d, if we were to plot a graph of β against d, we would expect a linear relationship. As d increases, β increases, which means the graph should slope upwards.
Given the options in the question, we need to identify which graph represents this direct relationship. The correct graph should show an increasing trend as the distance between the slits (d) increases.
After analyzing the options, the correct answer is the graph that shows an increasing curve between fringe width (β) and distance between the slits (d). This corresponds to the second option provided.
Topper's Solved these Questions
- MOCK TEST 6BOOK - CAREER POINTCHAPTER - MOCK TEST 6EXERCISE - Part (B) (CHEMISTRY)
30 Videos
- MOCK TEST 6BOOK - CAREER POINTCHAPTER - MOCK TEST 6EXERCISE - Part (B) (CHEMISTRY)
30 Videos
- MOCK TEST 5BOOK - CAREER POINTCHAPTER - MOCK TEST 5EXERCISE - PART (B)-CHEMISTRY
29 Videos
- MOCK TEST 7BOOK - CAREER POINTCHAPTER - MOCK TEST 7EXERCISE - PART (B) - CHEMISTRY
30 Videos
Similar Questions
In a YDSE experiment, the distance between the slits & the screen is 100cm. For a certain distance between the slits, an interference pattern is observed on the screen with the fringe width 0.25mm. When the distance between the slits is increased by Δd=1.2mm, the fringe width decreased to n=2/3 of the original value. In the final position, a thin glass plate of refractive index 1.5 is kept in front of one of the slits & the shift of central maximum is observed to be 20 fringe width. Find the thickness of the plate & wavelength of the incident light.
View SolutionIn Young's double slit experiment, while using a source of light of wavelength 4500 Å , the fringe width obtained is 0.4 cm. If the distance between the slits and the screen is reduced to half , calculate the new fringe width.
View Solution
Knowledge Check
In young's double slit experiment, if the distance between the slits is halved and the distance between the slits and the screen is doubled, the fringe width becomes
AunchangedBhalvedCdoubledDquadrupledIn Young's experiment the distance between the slits is reduced to half and the distance between the slit and screen is doubled then the fringe width
Awill not changeBwill become halfCwill be doubledDwill become four timesIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and screen is doubled. The fringe-width will :
AunchangedBhalvedCdoubledDquadrupled
In Young's double slit experiment, the separation between the slits is halved and the distance between the slits and screen is doubled. The fringe-width will :
View SolutionIn Young's double slit experiment, the sepcaration between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View SolutionIn the Young's experiment, the distance between slit and screen is doubled and the distance between the two slits is reduced to half. The fringe widht is
View SolutionIn Young's double slit experiment, the distance between sources is 1mm and distance between the screen and source is 1 m . If the fringe width on the screen is 0.06cm , then λ=
View Solution
