In a $Y D S E$ experiment, the distance between the slits $&$ the screen is $100 c m$ . For a certain distance between the slits, an interference pattern is observed on the screen with the fringe width $0.25 m m$ . When the distance between the slits is increased by $Δ d = 1.2 m m,$ the fringe width decreased to $n = 2 / 3$ of the original value. In the final position, a thin glass plate of refractive index $1.5$ is kept in front of one of the slits $&$ the shift of central maximum is observed to be $20$ fringe width. Find the thickness of the plate $&$ wavelength of the incident light.

Text Solution

Verified by Experts

The correct Answer is: $μ = 600 n m, t = 24 μ m$

Clearly $β_{\in i t i a l} = \frac{λ D}{d_{i}}$
$\Rightarrow 0.25 \times 10^{- 3} = \frac{λ}{d} \times 1 m$
$\Rightarrow \frac{λ}{d} = 2.5 \times 10^{- 4} \dots \dots \dots \dots . . (1)$
Afterwards :
$\frac{2}{3} β_{i} = \frac{λ D}{(d + Δ d)}$
$\Rightarrow \frac{λ}{d + Δ d} = \frac{2}{3} \times \frac{2.5 \times 10^{- 4}}{1} ... ... ... ... . . (2)$
Dividing $(1) and (2)$
$\frac{d + Δ d}{d} = \frac{3}{2} \Rightarrow d = 2 (Δ d) = 2.4 m m$ .
$& λ = 2.4 \times 2.5 \times 10^{- 7} m = 600 n m$ .
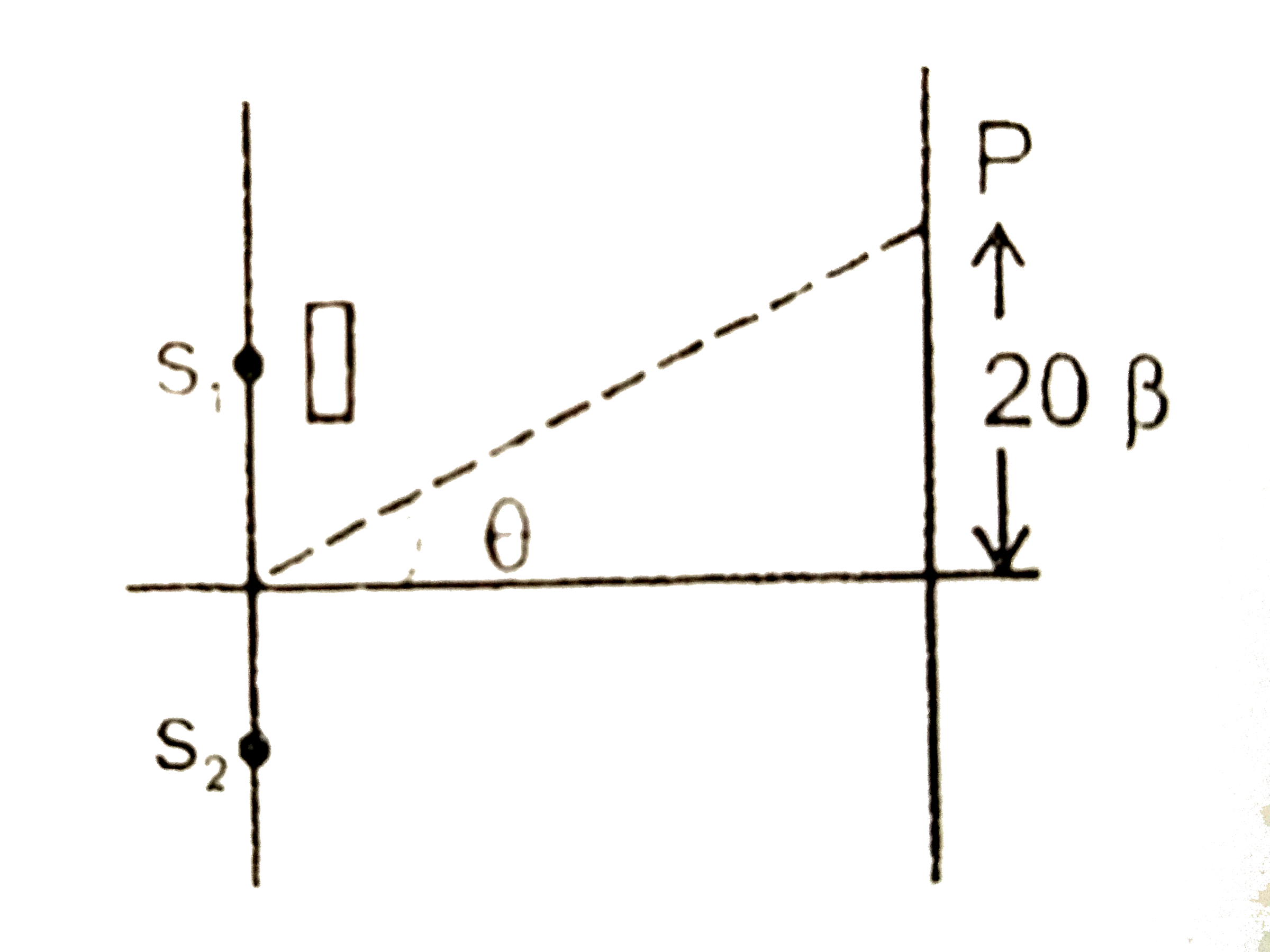
Now $P$ becomes central maxima.
$\Rightarrow$ for point $P : d sin θ = (μ - 1) t$
$\Rightarrow d . tan θ \approx (μ - 1) t$
$\Rightarrow d \frac{20 β}{D} = (μ - 1) t$
$\Rightarrow \frac{d}{D} \times \frac{20 \times λ D}{d} = (1.5 - 1) t$
$\Rightarrow t = \frac{20 λ}{0.5} = \frac{20 \times 600 \times 10^{- 9}}{0.5} = 24 μ m$ .

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In Young's experiment the distance between the slits is reduced to half and the distance between the slit and screen is doubled then the fringe width
Awill not change
Bwill become half
Cwill be doubled
Dwill become four times
Question 2 - Select One
In young's double slit experiment, if the distance between the slits is halved and the distance between the slits and the screen is doubled, the fringe width becomes
Aunchanged
Bhalved
Cdoubled
Dquadrupled
Question 3 - Select One
In a double experiment, the distance between the slit is 1 mm and screen is 25 cm away from the slits. The wavelength of light is $6000 Å$ . The width of the fringe on the screen is
A0.15 mm
B0.24 mm
C0.30 mm
D0.12 mm

RESONANCE-WAVE OPTICS-Advanced Level Problems

Home
Ask Doubt
Profile