A gas is expanded to double its volume by two different processes. One is isobaric and the other is isothermal. Let W1 and W2 be the respective work done, then find W1 and W2
W2=W1ln(2)
W2=Wln(2)
W2=W12
data is insufficient
The correct Answer is:A
W1=PdV=P(V2−V1)
⇒W1=PV1(V2V1−1)
=nRT(2−1)=nRT
W2=nRTln'V2V1nRTln2
W2=W1ln2
Topper's Solved these Questions
Similar Questions
Two identical containers contain same amount of ideal gas at identical condition. Gas is one container is expanded to 4 times of its volume at constant pressure and gas in another container is expanded to four times to its volume by isothermal process. If W1 and W2 be the respective work done, then W1W2=αIn2. Find 23α
View SolutionSome gas is enclosed in a piston-cylinder system. It is expanded to double its volume by isobaric or isothermal process. In which process more work is done by the gas.
View Solution
Knowledge Check
Two moles of a gas is expanded to double its volwne by two different processes. One is isobaric and the other is isothermal. If W1 and W2are the works done respectively, then
Aw2=W1ln2BW2=W1CW2=W1ln2DW21=W2ln2An ideal monatomic gas expands to twice its volume. If the process is isothermal, the magnitude of work done by the gas is W1. If the process is adiabatic, the magnitude of work done by the gas is Wa . Which of the following is true ?
AWi=Wa>0BWi>Wa=0CWi>Wa>0DWi>Wa>0The initial volume and pressure of a gas are V and P respectively. It is expand by two different processes such that in each process the final volume becomes 2V. If the work done in isothermal change is W1 and the amount of work done in adiabatic change isW2, then
AW1>W2BW1<W2CW1=W2Dnothing can be said
Consider the two process on a system as shown in figure. The volumes in the initial state and in the final state are the same in the two process A and B. If W1 and W2 be the work done by the system in the processes A and B respectively then-
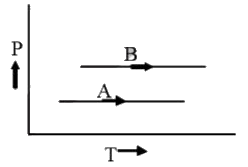
View SolutionW1,W2 and W3 are the different sizes of windows 1,2, and 3 respectively placed in a vertical plane. A particle is thrown up in the vertical plane. Let t1,t2 and t3 are the time taken to cross the window W1,W2 and W3 respectively and ΔV1,ΔV2 and ΔV3 are the change in speed after respective window cross.
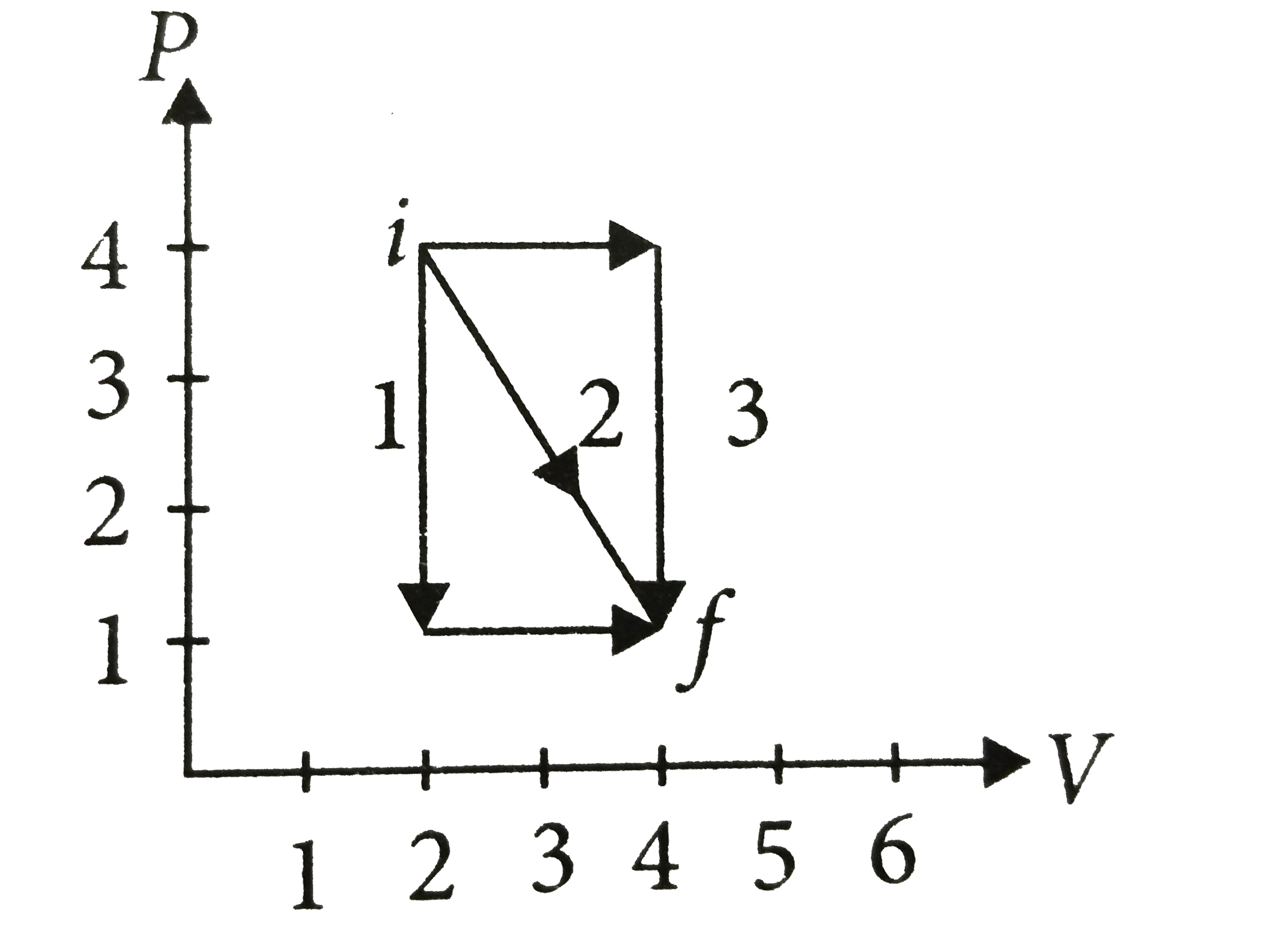
View SolutionA gas expands from i to f along the three paths indicated. The work done along the three paths denoted by W1,W2andW3 have the relationship
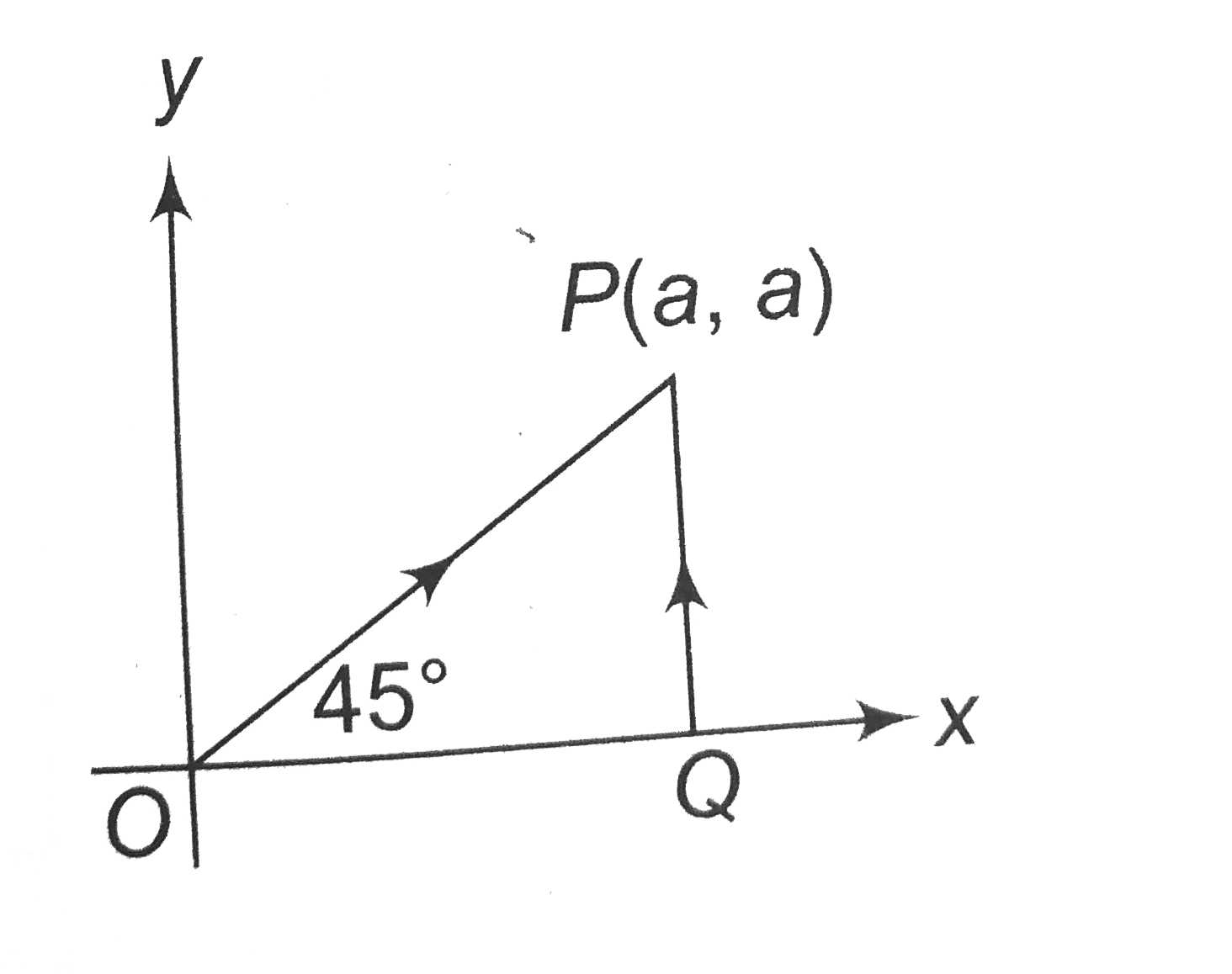
View SolutionA particle is moved from (0,0)to (a,a) under a force ¯¯¯F=(3ˆi+4ˆj) and path 2isOQP.Let W1andW2 be the work by done this force in these to paths .Then .
View SolutionA given mass of gas expands from state A to state B by three paths 1, 2 and 3 as shown in the figure
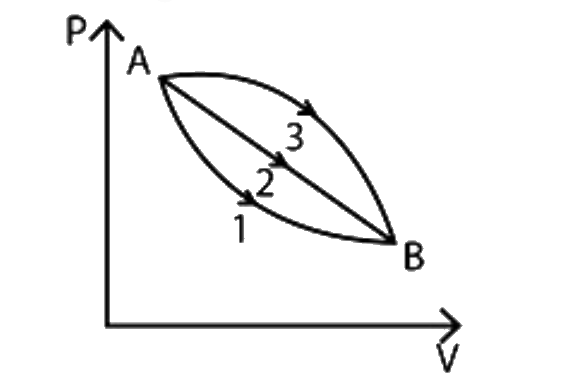
If w1,w2andw3 respectively are be the works done by the gas along three paths, then
View Solution
