Some gas is enclosed in a piston-cylinder system. It is expanded to double its volume by isobaric or isothermal process. In which process more work is done by the gas.
To determine which process (isobaric or isothermal) results in more work done by the gas when it expands to double its volume, we can analyze both processes step-by-step.
1. Understanding the Processes:
- Isobaric Process: This is a process that occurs at constant pressure. The work done by the gas during an isobaric expansion can be calculated using the formula:
Wisobaric=PΔV
where ΔV is the change in volume.
- Isothermal Process: This is a process that occurs at constant temperature. The work done by the gas during an isothermal expansion can be calculated using the formula:
Wisothermal=nRTln(V2V1)
where n is the number of moles of gas, R is the universal gas constant, T is the temperature, V1 is the initial volume, and V2 is the final volume.
2. Calculating Work Done in Isobaric Process:
- Let the initial volume V1=V0 and the final volume V2=2V0.
- The change in volume ΔV=V2−V1=2V0−V0=V0.
- Therefore, the work done in the isobaric process is:
Wisobaric=P⋅V0
3. Calculating Work Done in Isothermal Process:
- For the isothermal process, using the same initial and final volumes:
Wisothermal=nRTln(V2V1)=nRTln(2V0V0)=nRTln(2)
- The value of ln(2) is approximately 0.693.
4. Comparing the Two Work Values:
- We can express the work done in the isothermal process as:
Wisothermal=nRT⋅0.693
- To compare Wisothermal and Wisobaric, we note that:
- Wisobaric=P⋅V0
- Wisothermal=nRT⋅0.693
5. Conclusion:
- In general, for a given amount of gas and under the same conditions, the work done in the isobaric process is greater than that done in the isothermal process because the isobaric process allows for a larger change in volume at constant pressure compared to the logarithmic change in volume at constant temperature.
Final Answer:
More work is done by the gas in the isobaric process compared to the isothermal process.
- Isobaric Process: This is a process that occurs at constant pressure. The work done by the gas during an isobaric expansion can be calculated using the formula:
Wisobaric=PΔV
where ΔV is the change in volume.
- Isothermal Process: This is a process that occurs at constant temperature. The work done by the gas during an isothermal expansion can be calculated using the formula:
Wisothermal=nRTln(V2V1)
where n is the number of moles of gas, R is the universal gas constant, T is the temperature, V1 is the initial volume, and V2 is the final volume.
- Let the initial volume V1=V0 and the final volume V2=2V0.
- The change in volume ΔV=V2−V1=2V0−V0=V0.
- Therefore, the work done in the isobaric process is:
Wisobaric=P⋅V0
- For the isothermal process, using the same initial and final volumes:
Wisothermal=nRTln(V2V1)=nRTln(2V0V0)=nRTln(2)
- The value of ln(2) is approximately 0.693.
- We can express the work done in the isothermal process as:
Wisothermal=nRT⋅0.693
- To compare Wisothermal and Wisobaric, we note that:
- Wisobaric=P⋅V0
- Wisothermal=nRT⋅0.693
- In general, for a given amount of gas and under the same conditions, the work done in the isobaric process is greater than that done in the isothermal process because the isobaric process allows for a larger change in volume at constant pressure compared to the logarithmic change in volume at constant temperature.
More work is done by the gas in the isobaric process compared to the isothermal process.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Conceptual MCQs Single Option Correct21videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Numerical MCQs Single Options Correct42videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Practice Exercise 3.411videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems42videos
PHOTOELECTRIC EFFECT AND MATTER WAVES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems28videos
WAVE OPTICS
Similar Questions
A gas is taken through an isothermal process as shown.Find the work done by the gas
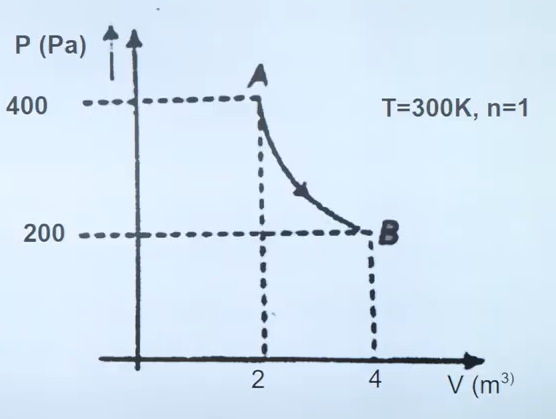 View Solution
View SolutionTwo samples A and B of the same gas have equal volumes and pressure. The gas in sample A is expanded isothermally to four times of its initial volume and the gas in B is expanded adiabatically to double its volume. It work done in isothermal process is twice that of adiabatic process, then show that γ satisfies the equation 1−21−γ=(γ−1)In2.
View Solution
Knowledge Check
- Question 1 - Select One
The thermodynamic process in which no work is done on or by the gas is
AIsothermal processBIsochoric processCAdiabatic processDIsobaric process - Question 2 - Select One
The thermodynamic process in which no work is done on or by the gas is
Aisothermal processBadiabatic processCisochoric processDisobaric process - Question 3 - Select One
An ideal gas is compressed to half its initial volume by means of several peocesses. Which of the process results in the maximum work done on the gas ?
AIsothermalBAdiabaticCIsobaricDIsochoric
An ideal gas is compressed to half its initial volume by means of several peocesses. Which of the process results in the maximum work done on the gas ?
View SolutionA gas expands isothermally and reversibly. The work done by the gas is
View SolutionIn an isothermal thermodynamical process, the value of work done by a system is
View SolutionA gas expands isothermally and reversibly. The work done by the gas is -
View SolutionIf one mole of gas doubles its volume at temperature T isothermally then work done by the gas is
View Solution

