For the Paschen series thr values of n1 and n2 in the expression ΔE=RHc[1n21−1n22] are
n1=1,n2=2,3,4
n1=2,n2=3,4,5
n1=3,n2=4,5,6
n1=4,n2=5,6,7
The correct Answer is:C
Step by step video, text & image solution for For the Paschen series thr values of n_(1) and n_(2) in the expression Delta E = R_(H)c [(1)/(n_(1)^(2))-(1)/(n_(2)^(2))] are by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - DINESH PUBLICATIONCHAPTER - ATOMIC STRUCTUREEXERCISE - Selected Straight Objective Type MCQs
70 Videos
- ATOMIC STRUCTUREBOOK - DINESH PUBLICATIONCHAPTER - ATOMIC STRUCTUREEXERCISE - Compre.
17 Videos
- ATOMIC STRUCTUREBOOK - DINESH PUBLICATIONCHAPTER - ATOMIC STRUCTUREEXERCISE - Ultimate Preparatory Package
15 Videos
- APPENDIXBOOK - DINESH PUBLICATIONCHAPTER - APPENDIXEXERCISE - Completion Reactions
15 Videos
- BIOMOLECULESBOOK - DINESH PUBLICATIONCHAPTER - BIOMOLECULESEXERCISE - Reason
1 Videos
Similar Questions
When electron jumps from higher orbit to lower orbit, then energy is radiated in the form of electromagnetic radiation and these radiations are used to record the emission spectrum Energy of electron may be calculated as
E=−2π2meZ2e4n2h2
Where, me= rest mass of electron
ΔE=(En2−En1)=13.6×Z2[1n21−1n22]eV per atom
This equation was also used by Rydberg to calculate the wave number of a particular line in the spectrum
¯v=1λ=RHZ2[1n21−1n22]m−1
Where RH=1.1×107m−1 (Rydberg constant)
For Lyman, Balmer, Paschen, Brackett and Pfund series the value of n1=1,2,3,4,5 respectively and n2=∞ for series limit. If an electron jumps from higher orbit n to ground state, then number of spectral line will be .nC2. Ritz modified the Rydberg equation by replacing the rest mass of electron with reduced mass (μ).
1μ=1mN+1me
Here, mN= mass of nucleus me= mass of electron Answer the following questions
The ratio of the wavelength of the first line to that of second line of Paschen series of H-atom is
View SolutionWhen electron jumps from higher orbit to lower orbit, then energy is radiated in the form of electromagnetic radiation and these radiations are used to record the emission spectrum Energy of electron may be calculated as
E=−2π2meZ2e4n2h2
Where, me= rest mass of electron
ΔE=(En2−En1)=13.6×Z2[1n21−1n22]eV per atom
This equation was also used by Rydberg to calculate the wave number of a particular line in the spectrum
¯v=1λ=RHZ2[1n21−1n22]m−1
Where RH=1.1×107m−1 (Rydberg constant)
For Lyman, Balmer, Paschen, Brackett and Pfund series the value of n1=1,2,3,4,5 respectively and n2=∞ for series limit. If an electron jumps from higher orbit n to ground state, then number of spectral line will be .nC2. Ritz modified the Rydberg equation by replacing the rest mass of electron with reduced mass (μ).
1μ=1mN+1me
Here, mN= mass of nucleus me= mass of electron Answer the following questions
If the wavelength of series limit of Lyman's series of He+ ions is ''a'' 0A, then what will be the wavelength of series limit of Lyman's series for Li2+ ion?
View Solution
Knowledge Check
For the Paschen series the values of n1 and n2 in the expression ΔE=RH.c(1n21−1n22)
An1=1,n2=2,3,4 …Bn1=2,n2=3,4,5Cn13,n2=4,5,6 …….Dn1=4,n2=5,6,7 ……For a single electron atom or ion the wave number of radiation emitted during the transition of electron from a higher energy state (n=n2) to a lower energy state (n=n1) is given by the expression:
¯v=1λ=RH.z2(1n21−1n22) ...(1)
where RH=2π2mk2e4h3c= Rydberg constant for H-atom
Where the terms have their usual meanings. Considering the nuclear motion, the most accurate expression would have been to replace mass of electron (m) by the reduced mass (μ) in the above expression, defined as
μ=m'.mm'+m where m'= mass of nucleus
For Lyman series: n1=1 (fixed for all the lines)
while n2=2,3,4... for successive lines i.e. 1st,2nd,3rd... lines, respectively. For Balmer series: n1=2 (fixed for all the lines) while n2=3,4,5... for successive lines.
The ratio of the wave numbers for the highest energy transition of e− in Lyman and Balmer series of H-atom is:A4:1B6:1C9:1D3:1For a single electron atom or ion the wave number of radiation emitted during the transition of electron from a higher energy state (n=n2) to a lower energy state (n=n1) is given by the expression:
¯v=1λ=RH.z2(1n21−1n22) ...(1)
where RH=2π2mk2e4h3c= Rydberg constant for H-atom
Where the terms have their usual meanings. Considering the nuclear motion, the most accurate expression would have been to replace mass of electron (m) by the reduced mass (μ) in the above expression, defined as
μ=m'.mm'+m where m'= mass of nucleus
For Lyman series: n1=1 (fixed for all the lines)
while n2=2,3,4... for successive lines i.e. 1st,2nd,3rd... lines, respectively. For Balmer series: n1=2 (fixed for all the lines) while n2=3,4,5... for successive lines.
If proton in H-nucleus be replaced by positron having the same mass as that of electron but same charge as that of proton, then considering the nuclear motion, the wavenumber of the lowest energy transition of He+ ion in Lyman series will be equal toA2RHB3RHC4RHDRH
When electron jumps from higher orbit to lower orbit, then energy is radiated in the form of electromagnetic radiation and these radiations are used to record the emission spectrum Energy of electron may be calculated as
E=−2π2meZ2e4n2h2
Where, me= rest mass of electron
ΔE=(En2−En1)=13.6×Z2[1n21−1n22]eV per atom
This equation was also used by Rydberg to calculate the wave number of a particular line in the spectrum
¯v=1λ=RHZ2[1n21−1n22]m−1
Where RH=1.1×107m−1 (Rydberg constant)
For Lyman, Balmer, Paschen, Brackett and Pfund series the value of n1=1,2,3,4,5 respectively and n2=∞ for series limit. If an electron jumps from higher orbit n to ground state, then number of spectral line will be .nC2. Ritz modified the Rydberg equation by replacing the rest mass of electron with reduced mass (μ).
1μ=1mN+1me
Here, mN= mass of nucleus me= mass of electron Answer the following questions
The emission spectrum of He+ involves transition of electron from n2→n1 such that n2+n1=8 and n2−n1=4. what whill be the total number of lines in the spectrum?
View SolutionThe emission spectrum of hydrogen is found to satisfy the expression for the energy change ΔE (in joules) such that
ΔE=2.18×10−18(1n21−1n22)J
where n1=1,2,3,.... and n2=2,3,4,... The spectral lines correspond to Paschen series if
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).
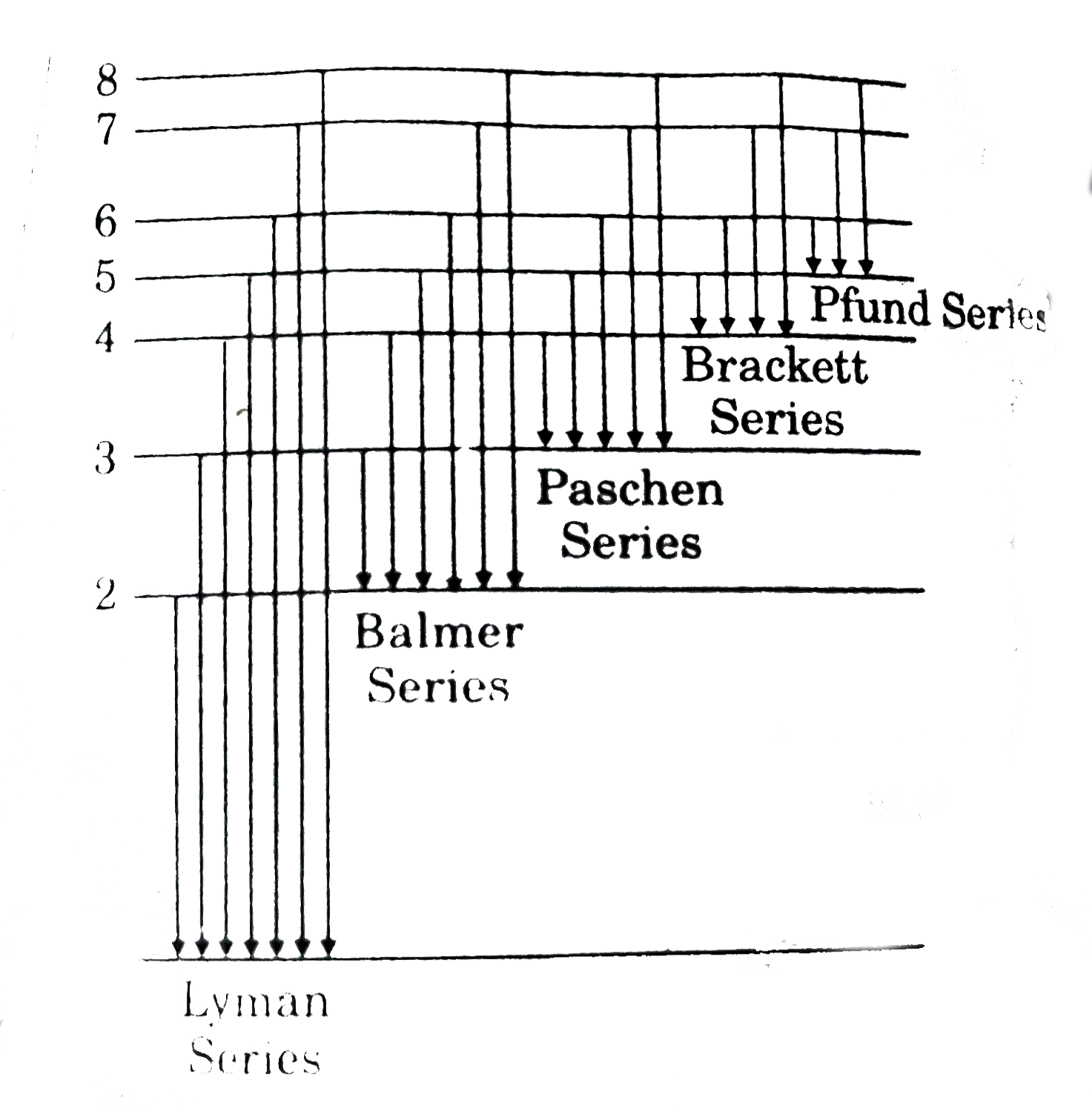
Maximum number of different lines produced when electron jump from nth level to ground level is equal to
n(n−1)2.
For example in the case of n=4, number of lines produced is 6.(4→3,4→2,4→1,3→2,3→1,2→1).When an electron returns from n2ton1 state, the number of different
lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as:
E2−E1=ΔE,λ=hcΔE,ΔE=hv(v−frequency)
Since h and c are constants ΔE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
¯v=RZ2(1n21−1n22)
where R is a Rydberg constant (R=1.1×107m−1).
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
wave number of the first line of Paschen series in Be3+ ion is :
View Solutionthe only electron in the hydrogen atom resides under ordinary conditions in the first orbit. When energy is supplied the electron moves to higher energy orbit depending on the amount of energy absorbed. It emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second. Similarly, Paschen, Breakett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively (as shown in figure).

Maximum number of different lines produced when electron jump from nth level to ground level is equal to
n(n−1)2.
For example in the case of n=4, number of lines produced is 6.(4→3,4→2,4→1,3→2,3→1,2→1).When an electron returns from n2ton1 state, the number of different
lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as:
E2−E1=ΔE,λ=hcΔE,ΔE=hv(v−frequency)
Since h and c are constants ΔE corresponds to definite energy: thus each transition from one energy level to another will produce a light of definite wavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula:
¯v=RZ2(1n21−1n22)
where R is a Rydberg constant (R=1.1×107m−1).
(i) First line of a series : It is called line of longest wavelength of line of smallest energy'.
(ii) Series limit or last line of a series : It is the line of shortest wavelength or line of highest energy.
Last line of breakett series for H-atom has wavelength λ1Å and 2nd line of Lyman series has wavelength λ2Åthen:
View SolutionThe only electron in the hydrogen atom resides under ordinary conditions on the first orbit. When energy is supplied, the electron moves to higher energy orbit depending on the amount of energy absorbed. When this electron returns to any of the lower orbits, it emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second orbit. Similarly, Paschen, Brackett and Pfund series are formed when electron returns to the third, fourth and fifth orbits from higher energy orbits respectively.
Maximum number of lines produced when an electron jumps from nth level to ground level is equal to n(n−1)2. For exampe, in the case of n=4, number of lines produced is 6(4→3,4t2,4→1,3→2,3→1,2→1). When an electron returns from n2 and n1 state, the number of lines in the spectrum will be equal to
(n2−n1)(n2−n1+12
If the electron comes back from energy level having energy E2 to energy level having energy E1, then the difference may be expressed in terms of energy of photon as :
E2−E1=ΔE,λ=hcΔE
Since h and c are constants, ΔE corresponds to definite energy, thus each transition from one energy level to another will produce a light of definitewavelength. This is actually observed as a line in the spectrum of hydrogen atom.
Wave number of line is given by the formula
→v=R(1n21−1n22), where R is a Rydberg's constant (R=1.1×107m−1)
The difference in the wavelength of the 1st line of Lyman series and 2nd line of Balmer series in a hydrogen atom is :
View Solution
