When electron jumps from higher orbit to lower orbit, then energy is radiated in the form of electromagnetic radiation and these radiations are used to record the emission spectrum Energy of electron may be calculated as
E=−2π2meZ2e4n2h2
Where, me= rest mass of electron
ΔE=(En2−En1)=13.6×Z2[1n21−1n22]eV per atom
This equation was also used by Rydberg to calculate the wave number of a particular line in the spectrum
¯v=1λ=RHZ2[1n21−1n22]m−1
Where RH=1.1×107m−1 (Rydberg constant)
For Lyman, Balmer, Paschen, Brackett and Pfund series the value of n1=1,2,3,4,5 respectively and n2=∞ for series limit. If an electron jumps from higher orbit n to ground state, then number of spectral line will be .nC2. Ritz modified the Rydberg equation by replacing the rest mass of electron with reduced mass (μ).
1μ=1mN+1me
Here, mN= mass of nucleus me= mass of electron Answer the following questions
If the wavelength of series limit of Lyman's series of He+ ions is ''a'' 0A, then what will be the wavelength of series limit of Lyman's series for Li2+ ion?
9a40A
4a90A
16a90A
4a70A
The correct Answer is:B
¯v=1λ=RHz2[1n21−1n22]
Topper's Solved these Questions
Similar Questions
Complete the following reaction
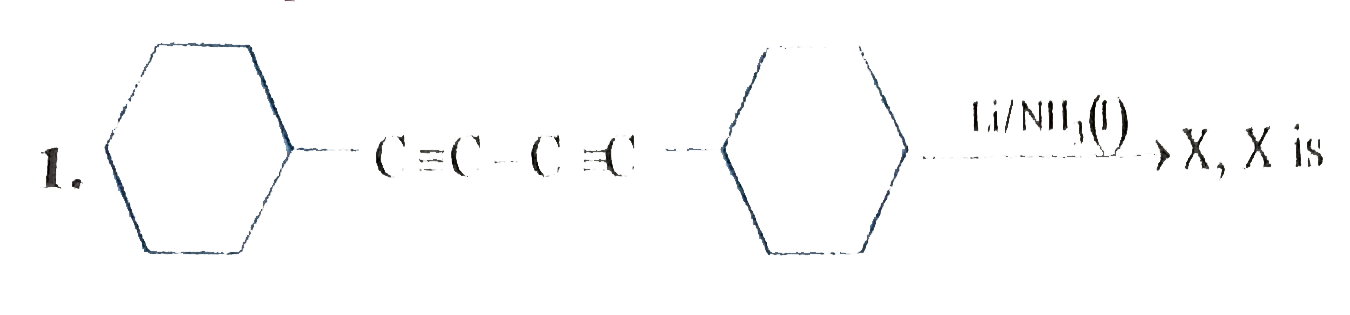
View Solution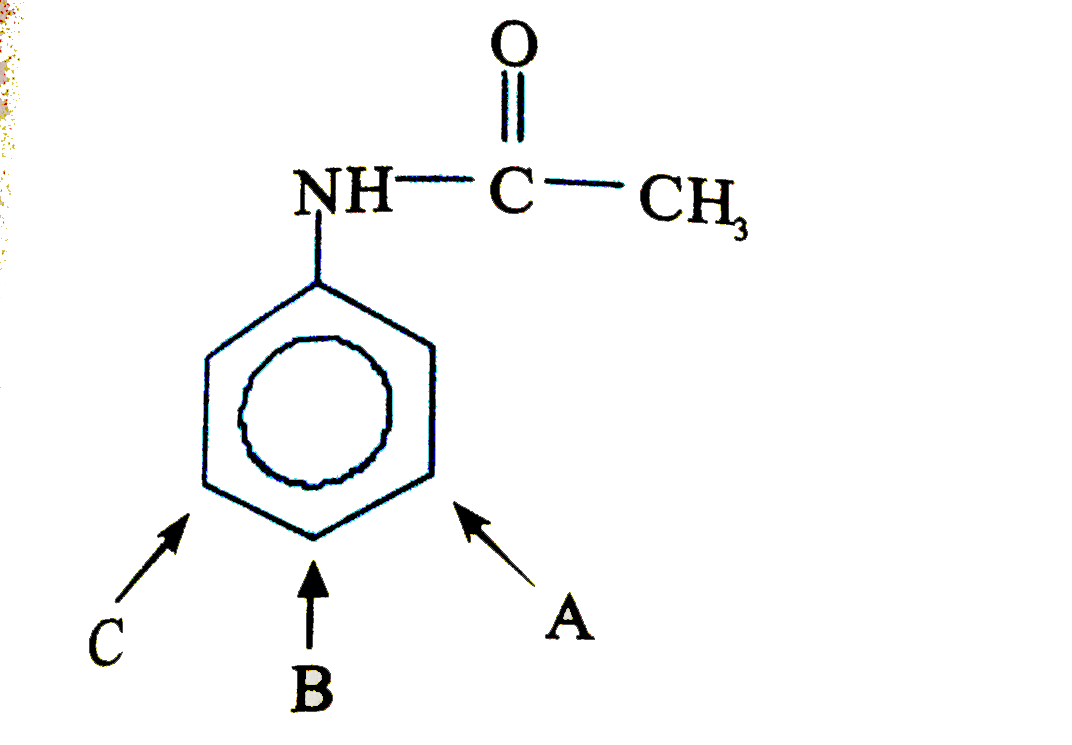
Identify the position where electrophilic aromatic substitution EAS) is most favourable
View SolutionWhen an electron jumps from n1thorbit→n_(2) th orbit, the energy radiated is given by
View SolutionWhen electron jumps from higher orbit to lower orbit, then energy is radiated in the form of electromagnetic radiation and these radiations are used to record the emission spectrum Energy of electron may be calculated as
E=−2π2meZ2e4n2h2
Where, me= rest mass of electron
ΔE=(En2−En1)=13.6×Z2[1n21−1n22]eV per atom
This equation was also used by Rydberg to calculate the wave number of a particular line in the spectrum
¯v=1λ=RHZ2[1n21−1n22]m−1
Where RH=1.1×107m−1 (Rydberg constant)
For Lyman, Balmer, Paschen, Brackett and Pfund series the value of n1=1,2,3,4,5 respectively and n2=∞ for series limit. If an electron jumps from higher orbit n to ground state, then number of spectral line will be .nC2. Ritz modified the Rydberg equation by replacing the rest mass of electron with reduced mass (μ).
1μ=1mN+1me
Here, mN= mass of nucleus me= mass of electron Answer the following questions
The emission spectrum of He+ involves transition of electron from n2→n1 such that n2+n1=8 and n2−n1=4. what whill be the total number of lines in the spectrum?
View SolutionWhen electron jumps from higher orbit to lower orbit, then energy is radiated in the form of electromagnetic radiation and these radiations are used to record the emission spectrum Energy of electron may be calculated as
E=−2π2meZ2e4n2h2
Where, me= rest mass of electron
ΔE=(En2−En1)=13.6×Z2[1n21−1n22]eV per atom
This equation was also used by Rydberg to calculate the wave number of a particular line in the spectrum
¯v=1λ=RHZ2[1n21−1n22]m−1
Where RH=1.1×107m−1 (Rydberg constant)
For Lyman, Balmer, Paschen, Brackett and Pfund series the value of n1=1,2,3,4,5 respectively and n2=∞ for series limit. If an electron jumps from higher orbit n to ground state, then number of spectral line will be .nC2. Ritz modified the Rydberg equation by replacing the rest mass of electron with reduced mass (μ).
1μ=1mN+1me
Here, mN= mass of nucleus me= mass of electron Answer the following questions
In which of the following region the spectrum of He+ will be observed in above transition?
View SolutionWhen electron jumps from higher orbit to lower orbit, then energy is radiated in the form of electromagnetic radiation and these radiations are used to record the emission spectrum Energy of electron may be calculated as E =- (2pi^(2)m_(e)Z^(2)e^(4))/(n^(2)h^(2)) Where, m_(e)= rest mass of electron DeltaE = (E_(n_(2))-E_(n_(1))) = 13.6 xx Z^(2) [(1)/(n_(1)^(2))-(1)/(n_(2)^(2))]eV per atom This equation was also used by Rydberg to calculate the wave number of a particular line in the spectrum bar(v) = (1)/(lambda) = R_(H)Z^(2) [(1)/(n_(1)^(2))-(1)/(n_(2)^(2))]m^(-1) Where R_(H) = 1.1 xx 10^(7)m^(-1) (Rydberg constant) For Lyman, Balmer, Paschen, Brackett and Pfund series the value of n_(1) = 1,2,3,4,5 respectively and n_(2) =oo for series limit. If an electron jumps from higher orbit n to ground state, then number of spectral line will be .^(n)C_(2) . Ritz modified the Rydberg equation by replacing the rest mass of electron with reduced mass (mu) . (1)/(mu) = (1)/(m_(N))+ (1)/(m_(e)) Here, m_(N)= mass of nucleus m_(e)= mass of electron Answer the following questions What will be the value of modified Rydberg's constant, if the nucleus having mass m_(N) and the electron having mass m_(e) revolve around the centre of the mass?
View SolutionWhen electron jumps from higher orbit to lower orbit, then energy is radiated in the form of electromagnetic radiation and these radiations are used to record the emission spectrum Energy of electron may be calculated as E =- (2pi^(2)m_(e)Z^(2)e^(4))/(n^(2)h^(2)) Where, m_(e)= rest mass of electron DeltaE = (E_(n_(2))-E_(n_(1))) = 13.6 xx Z^(2) [(1)/(n_(1)^(2))-(1)/(n_(2)^(2))]eV per atom This equation was also used by Rydberg to calculate the wave number of a particular line in the spectrum bar(v) = (1)/(lambda) = R_(H)Z^(2) [(1)/(n_(1)^(2))-(1)/(n_(2)^(2))]m^(-1) Where R_(H) = 1.1 xx 10^(7)m^(-1) (Rydberg constant) For Lyman, Balmer, Paschen, Brackett and Pfund series the value of n_(1) = 1,2,3,4,5 respectively and n_(2) =oo for series limit. If an electron jumps from higher orbit n to ground state, then number of spectral line will be .^(n)C_(2) . Ritz modified the Rydberg equation by replacing the rest mass of electron with reduced mass (mu) . (1)/(mu) = (1)/(m_(N))+ (1)/(m_(e)) Here, m_(N)= mass of nucleus m_(e)= mass of electron Answer the following questions The ratio of the wavelength of the first line to that of second line of Paschen series of H-atom is
View SolutionThe energy of nth orbit is given by
En=−Rhcn2
When electron jumpsfrom one orbit to another orbit then wavelength associated with the radiation is given by
1λ=RZ2(1n21−1n22)
The series that belongs to visible region is
View SolutionIf the electron in a hydrogen atom jumps from an orbit with level n_(1)=2 an orbit with level n_(2)=1 . The emitted radiation has a wavelength given by
View SolutionIf the electron in a hydrogen atom jumps from an orbit with level n2=3 to orbit with level n1=2, the emitted radiation has a wavelength given by .
View SolutionThe only electron in the hydrogen atom resides under ordinary conditions on the first orbit. When energy is supplied, the electron moves to higher energy orbit depending on the amount of energy absorbed. When this electron returns to any of the lower orbits, it emits energy. Lyman series is formed when the electron returns to the lowest orbit while Balmer series is formed when the electron returns to second orbit. Similarly, Paschen, Brackett and Pfund series are formed when electron returns to the third, fourth orbits from higher energy orbits respectively (as shown in figure)
Maximum number of lines produced when an electron jumps from nth level to ground level is equal to n(n−1)2. For example, in the case of n = 4, number of lines produced is 6. (4→3,4→2,4→1,3→2,3→1,2→1). When an electron returns from n2 to n1 state, the number of lines in the spectrum will be equal to (n2−n1)(n2−n1+1)2
If the electron comes back from energy level having energy E2 to energy level having energy E2 then the difference may be expressed in terms of energy of photon as E2−E1=ΔE,λ=hcΔE. Since h and c are constant, ΔE corresponds to definite energy, thus each transition from one energy level to another will prouce a higher of definite wavelength. THis is actually observed as a line in the spectrum of hydrogen atom. Wave number of the line is given by the formula ¯v=RZ2(1n21−1n22)
Where R is a Rydberg constant (R=1.1×107)
(i) First line of a series : it is called .line of logest wavelength. or .line of shortest energy..
(ii) Series limit of last of a series : It is the line of shortest wavelength or line of highest energy.
The wave number of electromagnetic radiation emitted during the transition of electron in between two levels of Li2+ ion whose principal quantum numbers sum if 4 and difference is 2 is
View SolutionAccording to the Bohr theory for the atomic spectrum of hydrogen the energy levels of the proton -electron system depends, on the quantum number n. In an electron transition from a higher quantum level , n_(2) to the lower level n_(1) , radiation is emitted. The frequency, v of the radiation is given by h v = (E_(n_(2)) - E_(n_(1))) where, h is Planck.s constant and E_(n_(2)), E_(n_(1)) are the energy level values for the quantum number n_(2) and n_(1) . A useful formula for the wavelength, lambda = c//v is given by = lambda(Å) = (912)/(Z^(2)) xx ((n_(2)^(2)n_(1)^(2))/(n_(2)^(2)-n_(1)^(2))) where, Z = atomic number of any one electron species viz H, He^(+), Li^(2+), Be^(3+) ,..... For hydrogen Z=1 In the above formula, when n_(2) rarr oo , we have lambda = (912)/(1^(2)) xx n_(1)^(2) . This values of lambda is known as the series limit for the given value of n_(1) . Calculate the value of n_(1) for the series limit lambda = 8208 Å
View SolutionAccording to the Bohr theory for the atomic spectrum of hydrogen the energy levels of the proton -electron system depends, on the quantum number n. In an electron transition from a higher quantum level , n_(2) to the lower level n_(1) , radiation is emitted. The frequency, v of the radiation is given by h v = (E_(n_(2)) - E_(n_(1))) where, h is Planck.s constant and E_(n_(2)), E_(n_(1)) are the energy level values for the quantum number n_(2) and n_(1) . A useful formula for the wavelength, lambda = c//v is given by = lambda(Å) = (912)/(Z^(2)) xx ((n_(2)^(2)n_(1)^(2))/(n_(2)^(2)-n_(1)^(2))) where, Z = atomic number of any one electron species viz H, He^(+), Li^(2+), Be^(3+) ,..... For hydrogen Z=1 Calculating n_(2) for the series limit = 22800 Å. Calculate lambda for the transition (n_(2) + 1) to (n_(1) - 1)
View SolutionWhen electron jumps from higher orbit to lower orbit, then energy is radiated in the form of electro magnetic radiation and these radiations are used to record the emission spectrum Energy of electron may be calculated as E= (2pi^2 m_e Z^2 e^4)/(n^2 h^2) where m_e = rest mass of electron DeltaE = (E_(n_2)- E_(n_1)) = 13.6xxZ^2 xx [1/(n_1^2) - 1/(n_2^2)] eV per atom This equation was also used by Rydberg to calculate the wave number of a particular line in the spectrum. bar(upsilon) = 1/(lambda) = R_H Z^2 [1/(n_1^2) -1/n_2^2] m^(-1) Where , R_H = 1.1 xx 10^7 m^(-1) (Rydberg constant) For Lyman, Balmer, Paschen, Brackett and Pfund series the value of n_1 = 1,2,3,4,5 respectively and n_2 = oo for series limit, If an electron jumps from higher orbit n to ground state than number of spectral line will be ""^nC_2 . Ritz modified the Rydberg equation by replacing the rest mass of electron with reduced mass (mu) . 1/(mu) = 1/(m_N) + 1/(m_e) , Here m_N mass of nucleus , m_e = mass of electron. The emission spectrum of He^+ involves transition of electron from n_1 to n_2 such that n_2 + n_1 = 8 and n_2 - n_1 = 4 . What will be the total number of lines in the spectrum ?
View SolutionWhen electron jumps from higher orbit to lower orbit, then energy is radiated in the form of electro magnetic radiation and these radiations are used to record the emission spectrum Energy of electron may be calculated as E= (2pi^2 m_e Z^2 e^4)/(n^2 h^2) where m_e = rest mass of electron DeltaE = (E_(n_2)- E_(n_1)) = 13.6xxZ^2 xx [1/(n_1^2) - 1/(n_2^2)] eV per atom This equation was also used by Rydberg to calculate the wave number of a particular line in the spectrum. bar(upsilon) = 1/(lambda) = R_H Z^2 [1/(n_1^2) -1/n_2^2] m^(-1) Where , R_H = 1.1 xx 10^7 m^(-1) (Rydberg constant) For Lyman, Balmer, Paschen, Brackett and Pfund series the value of n_1 = 1,2,3,4,5 respectively and n_2 = oo for series limit, If an electron jumps from higher orbit n to ground state than number of spectral line will be ""^nC_2 . Ritz modified the Rydberg equation by replacing the rest mass of electron with reduced mass (mu) . 1/(mu) = 1/(m_N) + 1/(m_e) , Here m_N mass of nucleus , m_e = mass of electron. What will be the value of modified Rydberg.s constant, if the nucleus having mass m_N and the electron having mass m_e revolve around the centrer of the mass?
View Solution
