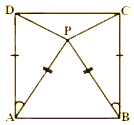
\n the following diagrams, ABCD is a square and APB is an equilateral triangle.In each case ,(1) Prove that : △ APD = △ BPC (ii) Find the angles of △ DPC.
Step by step video & image solution for \n the following diagrams, ABCD is a square and APB is an equilateral triangle.In each case ,(1) Prove that : triangle APD = triangle BPC (ii) Find the angles of triangle DPC. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In the given figure, P is any point located in the interior of the parallelogram ABCD. Indicate that (i) ar (Delta APB ) + ar (Delta PCD ) = (1)/(2) (ar||^(g m)ABCD) (Ii) ar(Delta APD) + ar(Delta BPC ) = ar(Delta APB) + ar(Delta PCD)
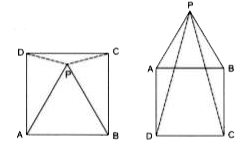
View SolutionIn the adjacent figure ABCD is a square and ΔAPB is an equilateral triangle. Prove thatΔAPD≅ΔBPC.
View SolutionABCD is a square and DEC is an equilateral triangle. Prove that AE = BE.
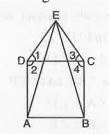
View SolutionABCD is square . BCE is equilateral Δ outside . Find ∠DEC
View SolutionIn the following diagrams, ABCD is a square and APB is an equilateral triangle. In each case,
(i) Prove that : ΔAPD≅ΔBPC
(ii) Find the angles of ΔDPC
View SolutionABCD is a quadrilateral and its diagonals AC and BD intersect each other at a point then prove that ar (Delta APB) xx ar (CPD) = ar (Delta APD) xx ar (Delta BPC)
View SolutionABCD is a square and DEC is an equilateral triangle. Prove that AE = BE.

View SolutionThe equilateral triangle ABP lies inside the square ABCD. Find ∠CPD.
View Solution
