క్రింది పటంలో ABCD ఒక చతురస్రము మరియు ΔAPB ఒక సమబాహు త్రిభుజము అయిన ΔAPD≅ΔBPCఅని నిరూపించుము. (సూచన:ΔAPDΔBPC లలో ¯¯¯AD=¯¯¯BC,¯¯¯AP=¯¯¯BP మరియు ∠PAD=∠PBC=90∘−60∘=30∘)
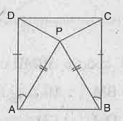
Step by step video & image solution for క్రింది పటంలో ABCD ఒక చతురస్రము మరియు Delta APB ఒక సమబాహు త్రిభుజము అయిన Delta APD ~= Delta BPCఅని నిరూపించుము. (సూచన:Delta APD Delta BPC లలో bar AD = bar BC, bar AP = bar BP మరియు /_PAD = /_PBC = 90^@ -60^@=30^@) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- త్రిభుజాలుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - త్రిభుజాలుEXERCISE - Exercise
89 Videos
- జ్యామితీయ మూలాలుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - జ్యామితీయ మూలాలుEXERCISE - Exercise
47 Videos
- నిరూపక జ్యామితిBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - నిరూపక జ్యామితిEXERCISE - Exercise
87 Videos
Similar Questions
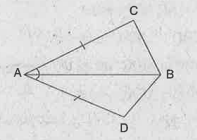
చతుర్భుజం ABCD లో , AC=AD మరియి ∠A కు AB కోన సమద్విఖండన రేఖ అయిన ΔABC=ΔABD అని చూపండి. BC మరియు BD ల గురించి మీరు ఏమి చెప్పగలరు?
View Solutionకింది వానికి జవాబులు ఇవ్వండి. ఘనాలకు ఎన్ని కొలతలు ఉంటాయి?
View Solutionఒక ఆవాస ప్రాంతంలో ప్రధాన రహదారి ఉత్తర-దక్షిణ దిశలలో ఉంది. దాని పటం కింది ఇవ్వబడినది. పటం సహాయంతో కింది ప్రశ్నలకు సమాధానాలు వ్రాయండి.
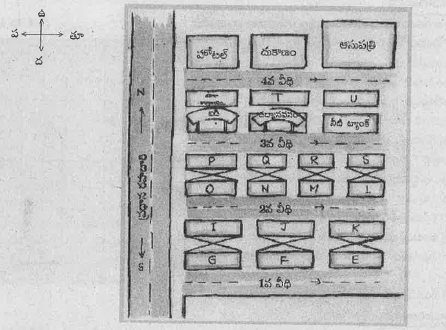 తూర్పుదిక్కున వెళ్లునప్పుడు మూడవవీధిలో ఎడమవైపు మూడోవస్థానంలో ఏం ఉంది?
తూర్పుదిక్కున వెళ్లునప్పుడు మూడవవీధిలో ఎడమవైపు మూడోవస్థానంలో ఏం ఉంది?
View SolutionABC is an equilateral triangle of side ‘a'. Then bar(AB).bar(BC) +bar(BC).bar(CA)+ bar(CA).bar(AB) =
View Solution\n the following diagrams, ABCD is a square and APB is an equilateral triangle.In each case ,(1) Prove that : triangle APD = triangle BPC (ii) Find the angles of triangle DPC.
View SolutionIn the figure given below, bar(ED)||bar(AB) and bar(EF)||bar(BC) . If /_FED =40^(@) and /_ DEC =20^(@) , then the angle made by bar(BC) at the centre is
View SolutionMatch the following Column A to Column B

View SolutionIn the given figure, ¯¯¯¯¯¯AD and ¯¯¯¯¯¯BE intersect at C, such that BC = CE, ∠ABC=40∘ and ∠DEC=85∘. Find ∠BAC−∠CDE.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E04_027_Q01.png" width="80%"gt
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionFind out area of triangle OAB and BCD shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_014_Q01.png" width="80%"gt
View SolutionThe resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R01_E02_023_Q01.png" width="80%"gt
View SolutionIn the following diagram AB, CDs are denominated at P, where BP = PC Delta APD And Delta BPC S
View SolutionIn the given figure, P is any point located in the interior of the parallelogram ABCD. Indicate that (i) ar (Delta APB ) + ar (Delta PCD ) = (1)/(2) (ar||^(g m)ABCD) (Ii) ar(Delta APD) + ar(Delta BPC ) = ar(Delta APB) + ar(Delta PCD)
View SolutionABC is an equitateral triangle of side 'a'. Then ¯¯¯¯¯¯AB.¯¯¯¯¯¯BC+¯¯¯¯¯¯BC.¯¯¯¯¯¯CA+¯¯¯¯¯¯CA.¯¯¯¯¯¯AB=
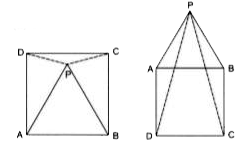
View SolutionIn the following diagrams, ABCD is a square and APB is an equilateral triangle. In each case,
(i) Prove that : ΔAPD≅ΔBPC
(ii) Find the angles of ΔDPC
View Solution
