Potential energy of a particle is related to x coordinate by equation x2−2x . Particle will be in stable equilibrium at :
x=0.5
x=1
x=2
x=4
The correct Answer is:B
To determine the position of stable equilibrium for a particle whose potential energy U is given by the equation U(x)=x2−2x, we can follow these steps:
Step 1: Understand the concept of stable equilibrium
Stable equilibrium occurs when the net force acting on the particle is zero, and the potential energy has a local minimum at that point.
Step 2: Relate force to potential energy
The force F acting on the particle can be derived from the potential energy using the equation:
F=−dUdx
Step 3: Differentiate the potential energy function
Given the potential energy function:
U(x)=x2−2x
we differentiate it with respect to x:
dUdx=2x−2
Step 4: Set the force to zero for equilibrium
For stable equilibrium, we set the force equal to zero:
F=−dUdx=0
This implies:
−(2x−2)=0
or:
2x−2=0
Step 5: Solve for x
Solving the equation 2x−2=0:
2x=2⟹x=1
Step 6: Confirm stability
To confirm that this point is indeed a point of stable equilibrium, we can check the second derivative of the potential energy:
d2Udx2=ddx(2x−2)=2
Since the second derivative is positive (d2Udx2>0), this indicates that the potential energy has a local minimum at x=1, confirming stable equilibrium.
Final Answer
The particle will be in stable equilibrium at x=1.
---
Stable equilibrium occurs when the net force acting on the particle is zero, and the potential energy has a local minimum at that point.
The force F acting on the particle can be derived from the potential energy using the equation:
F=−dUdx
Given the potential energy function:
U(x)=x2−2x
we differentiate it with respect to x:
dUdx=2x−2
For stable equilibrium, we set the force equal to zero:
F=−dUdx=0
This implies:
−(2x−2)=0
or:
2x−2=0
Solving the equation 2x−2=0:
2x=2⟹x=1
To confirm that this point is indeed a point of stable equilibrium, we can check the second derivative of the potential energy:
d2Udx2=ddx(2x−2)=2
Since the second derivative is positive (d2Udx2>0), this indicates that the potential energy has a local minimum at x=1, confirming stable equilibrium.
The particle will be in stable equilibrium at x=1.
Similar Questions
Knowledge Check
Potential energy of a particle at position x is given by U=(x2−4x)J. Which of the following is equilibrium position of the particle?
Ax=0Bx=5mCx=2mDx=4mPotential energy of a particle at position x is given by U=x2−5x. Which of the following is equilibrium position of the particle?
Ax=0Bx=5Cx=2.5Dx=7.5The potential energy of a particle (Ux) executing SHM is given by
AUx=K2(x−x0)2BUx=K1x+K2x2+K3x3CUx=Ae−bxDUx= constant
The potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionIn the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
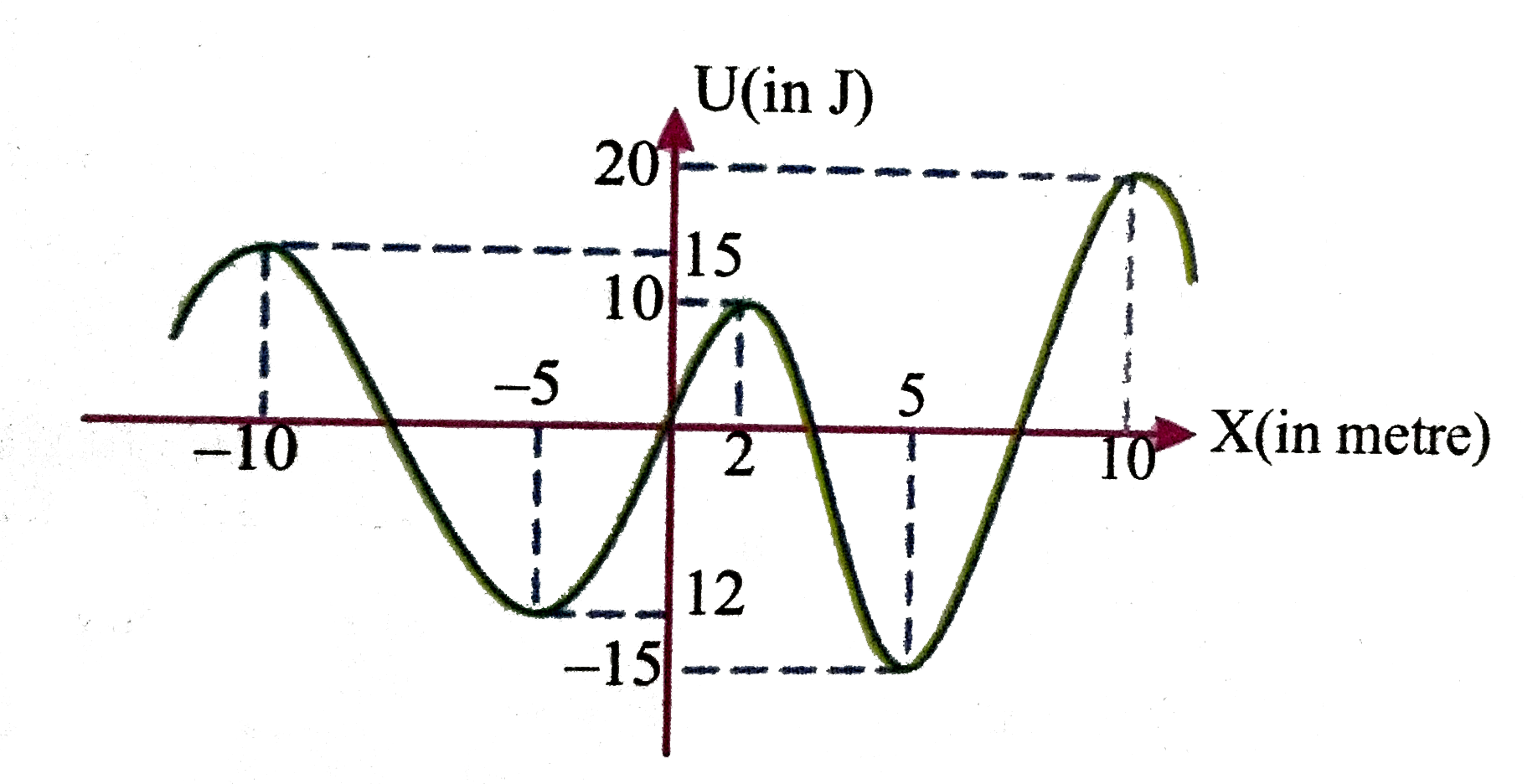
If the particle is released at the origin then
View SolutionThe potential energy of a particle varies with x according to the reltiaon U(x) =x2−4x. The point x =2 is a point of
View SolutionIn the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
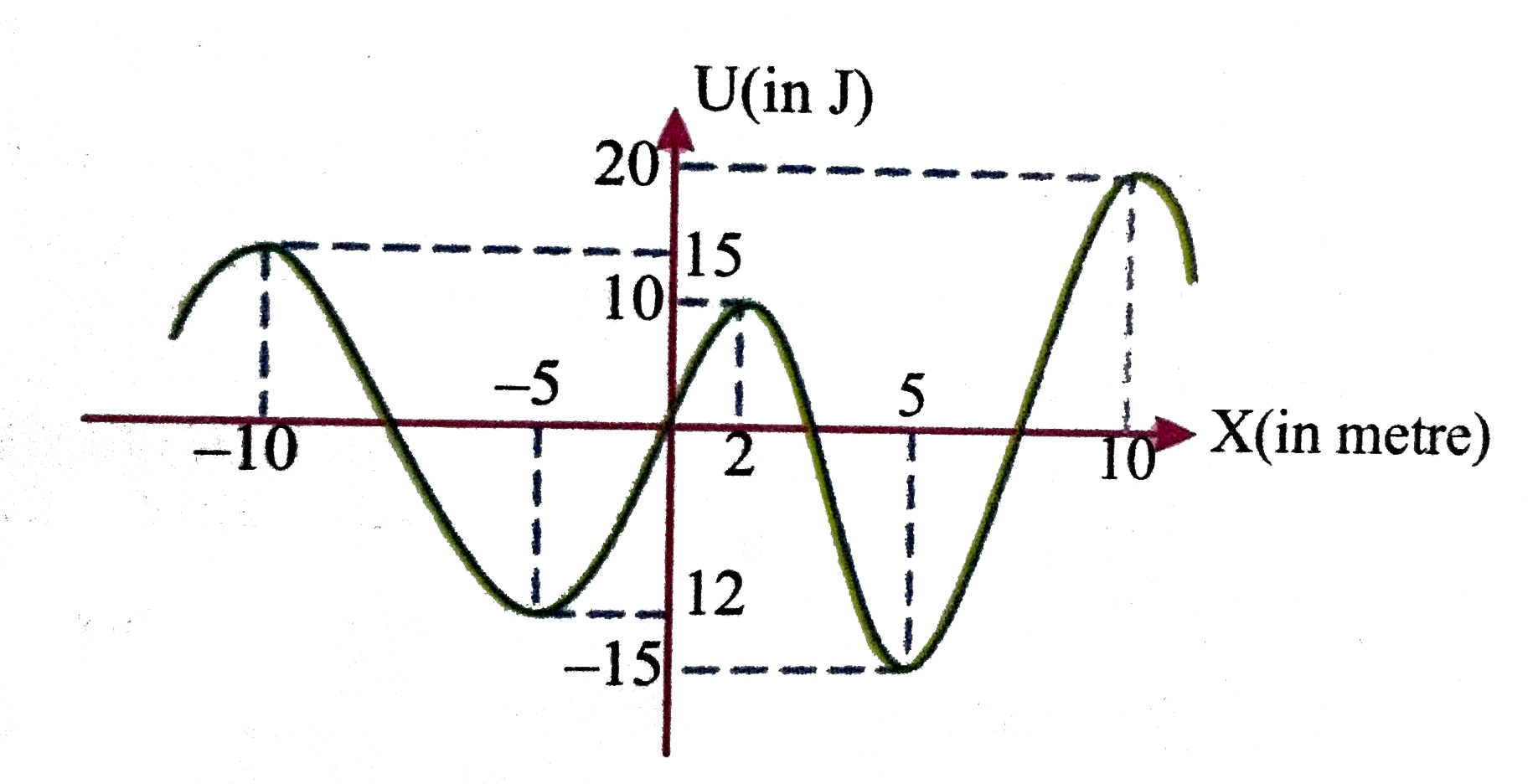
x=−5m and x=10m position of the particle are respectively of
View SolutionIn the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
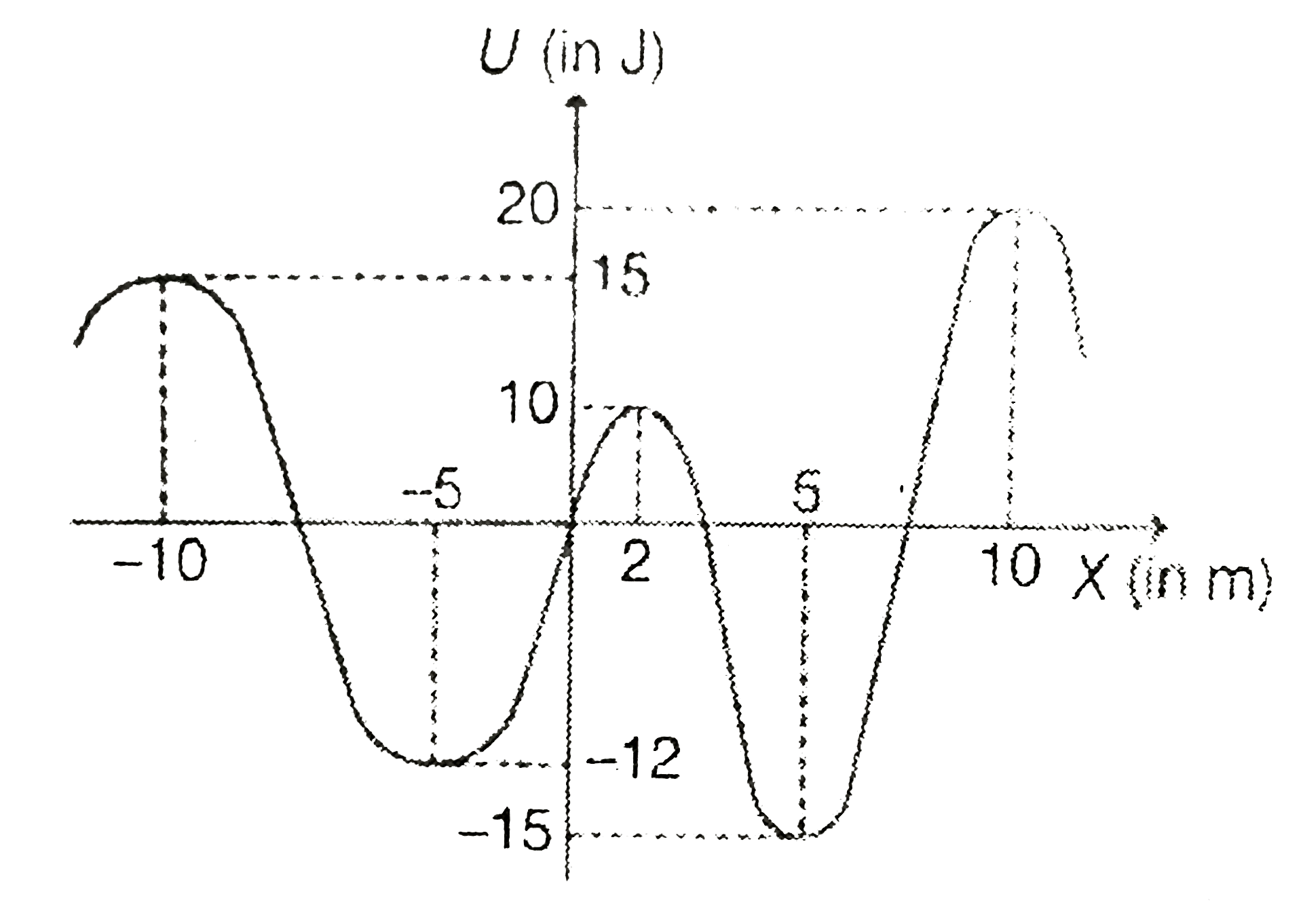
If the particle is released at the origin, then
View Solution
