Potential energy of a particle at position x is given by U=x2−5x. Which of the following is equilibrium position of the particle?
x=0
x=5
x=2.5
x=7.5
The correct Answer is:C
To determine the equilibrium position of a particle given its potential energy function U(x)=x2−5x, we will follow these steps:
Step 1: Understand the concept of equilibrium
In mechanics, a particle is in equilibrium when the net force acting on it is zero. The net force can be derived from the potential energy function.
Step 2: Relate force to potential energy
The force F acting on the particle is related to the potential energy U by the equation:
F=−dUdx
This means we need to find the derivative of the potential energy function with respect to x.
Step 3: Differentiate the potential energy function
Given:
U(x)=x2−5x
We differentiate U with respect to x:
dUdx=ddx(x2)−ddx(5x)=2x−5
Step 4: Find the expression for force
Using the relationship from Step 2:
F=−dUdx=−(2x−5)=−2x+5
Step 5: Set the force to zero for equilibrium
For equilibrium, we set the force F to zero:
−2x+5=0
Step 6: Solve for x
Rearranging the equation gives:
2x=5⟹x=52=2.5
Conclusion
Thus, the equilibrium position of the particle is at x=2.5.
In mechanics, a particle is in equilibrium when the net force acting on it is zero. The net force can be derived from the potential energy function.
The force F acting on the particle is related to the potential energy U by the equation:
F=−dUdx
This means we need to find the derivative of the potential energy function with respect to x.
Given:
U(x)=x2−5x
We differentiate U with respect to x:
dUdx=ddx(x2)−ddx(5x)=2x−5
Using the relationship from Step 2:
F=−dUdx=−(2x−5)=−2x+5
For equilibrium, we set the force F to zero:
−2x+5=0
Rearranging the equation gives:
2x=5⟹x=52=2.5
Thus, the equilibrium position of the particle is at x=2.5.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)
67 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
39 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
14 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
The potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x)J. The equilibrium position of the particle is at x m. The value of 10 x will be
View Solution
Knowledge Check
Potential energy of a particle at position x is given by U=(x2−4x)J. Which of the following is equilibrium position of the particle?
Ax=0Bx=5mCx=2mDx=4mThe potential energy of a particle (Ux) executing SHM is given by
AUx=K2(x−x0)2BUx=K1x+K2x2+K3x3CUx=Ae−bxDUx= constantIn the figure shown the potential energy U of a particle is plotted its position 'x' from origin. Then which of the following statement is correct A particle at :
 Ax1 is in stable equilibriumBx2 is in stable equilibriumCx3 is in stable equilibriumDnone of these
Ax1 is in stable equilibriumBx2 is in stable equilibriumCx3 is in stable equilibriumDnone of these
The potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionIn the fig. The potential energy U of a particle plotted against its position x from origin. Which of the following statement is correct
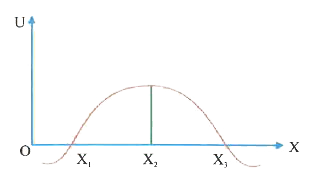
View SolutionThe potential energy of a conservative system is given by V(x)=(x2–3x) joule. Then its equilibrium position is at
View SolutionThe potential energy of a particle oscillating on x-axis is given as U+20+(x−2)2. The mean position is at
View Solution
