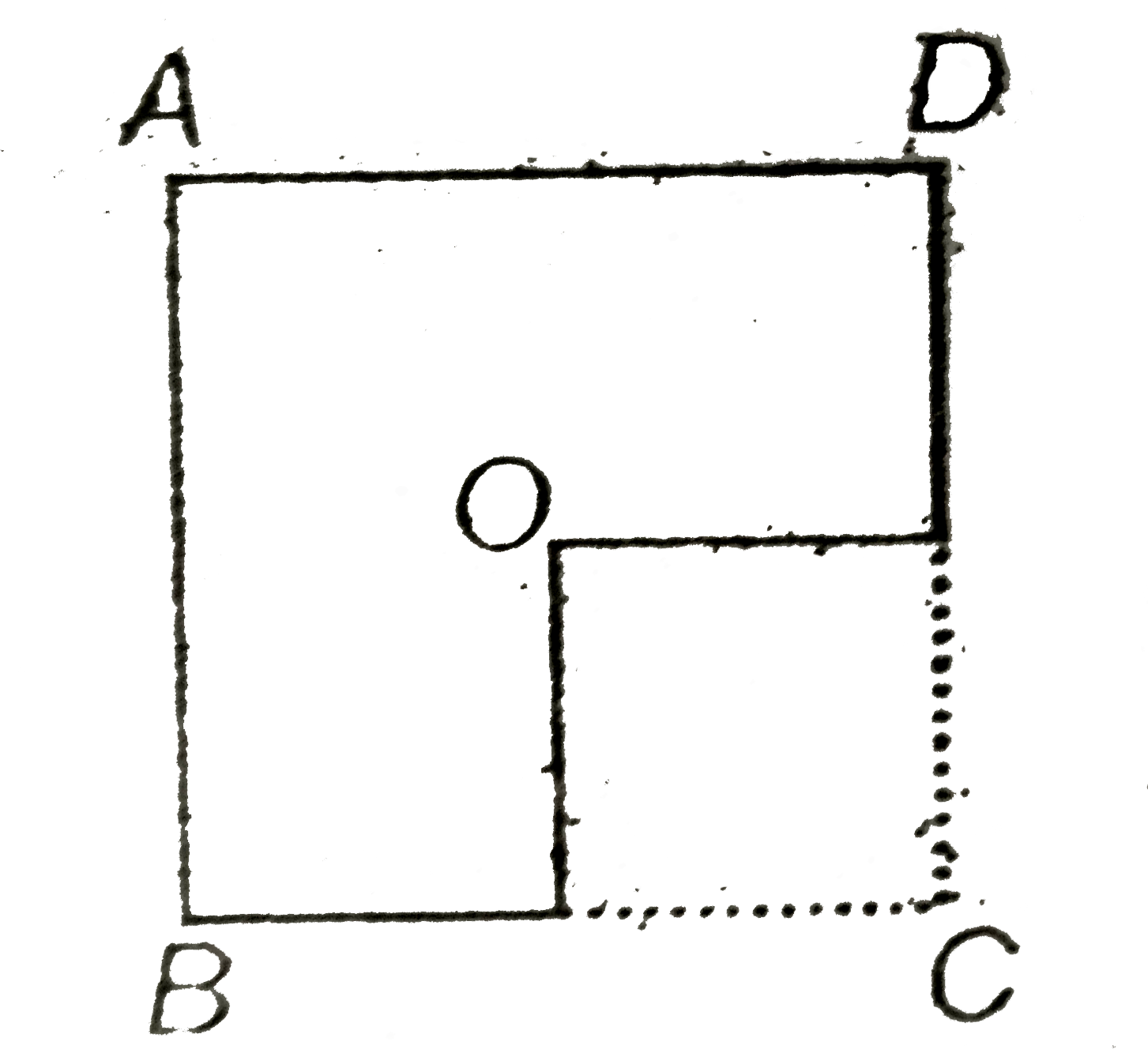
A square of side 4 cm and of uniform thickness is divided into four equal squares. If one of them is cut off (OECF), then the position of the centre of mass of the remaining portion from O is √2kcm . Find the value of K.
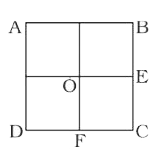
The correct Answer is:3
Let σ be surface mass density. The mass of the removed portion may be taken as negative. The given system may be regarded as two-particle system—one particle of mass 16σ at (0, 0) and second particle of mass '−4σ' at (1 , -1).
Now, x=16σ×0−4σ(1)12σ=−13cmandy=16σ×0−4σ(−1)12σ=13cm
r=√(−13)2+(13)2cm=√23cm.
Similar Questions
A square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find
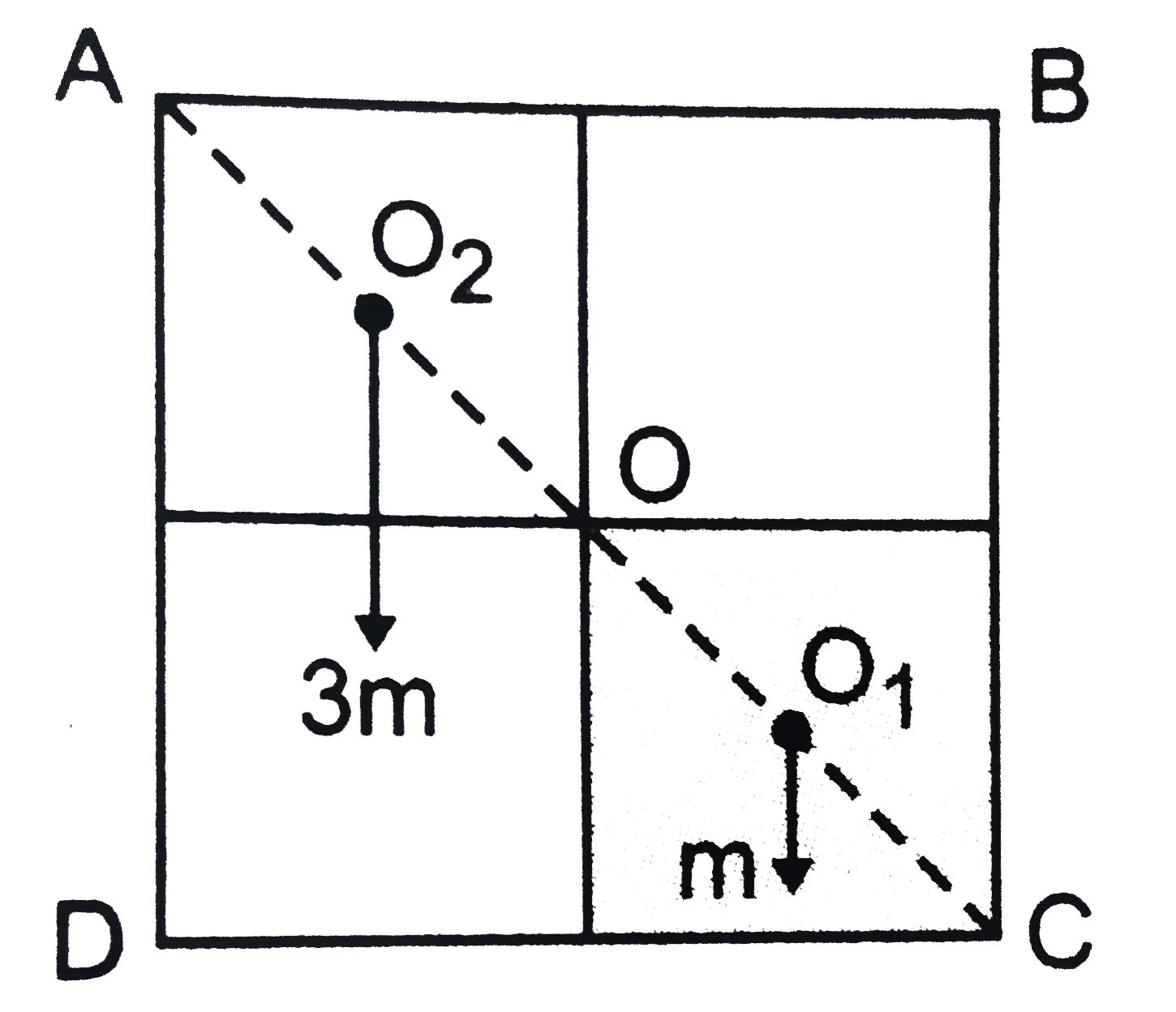
the position of centre of mass of the remaining portion from the centre O.View SolutionA uniform circular plate of uniform thickness has a diameter of 56 cm. A circular portion of diameter 42 cm is removed from the edge of the plate. Find the position of the centre of mass of the remaining portion.
View Solution
Knowledge Check
- Question 1 - Select One
A square of side a and uniform thickness is divided into four equal parts. If upper right part is removed, then find the coordinates of centre of mass of remaining part.
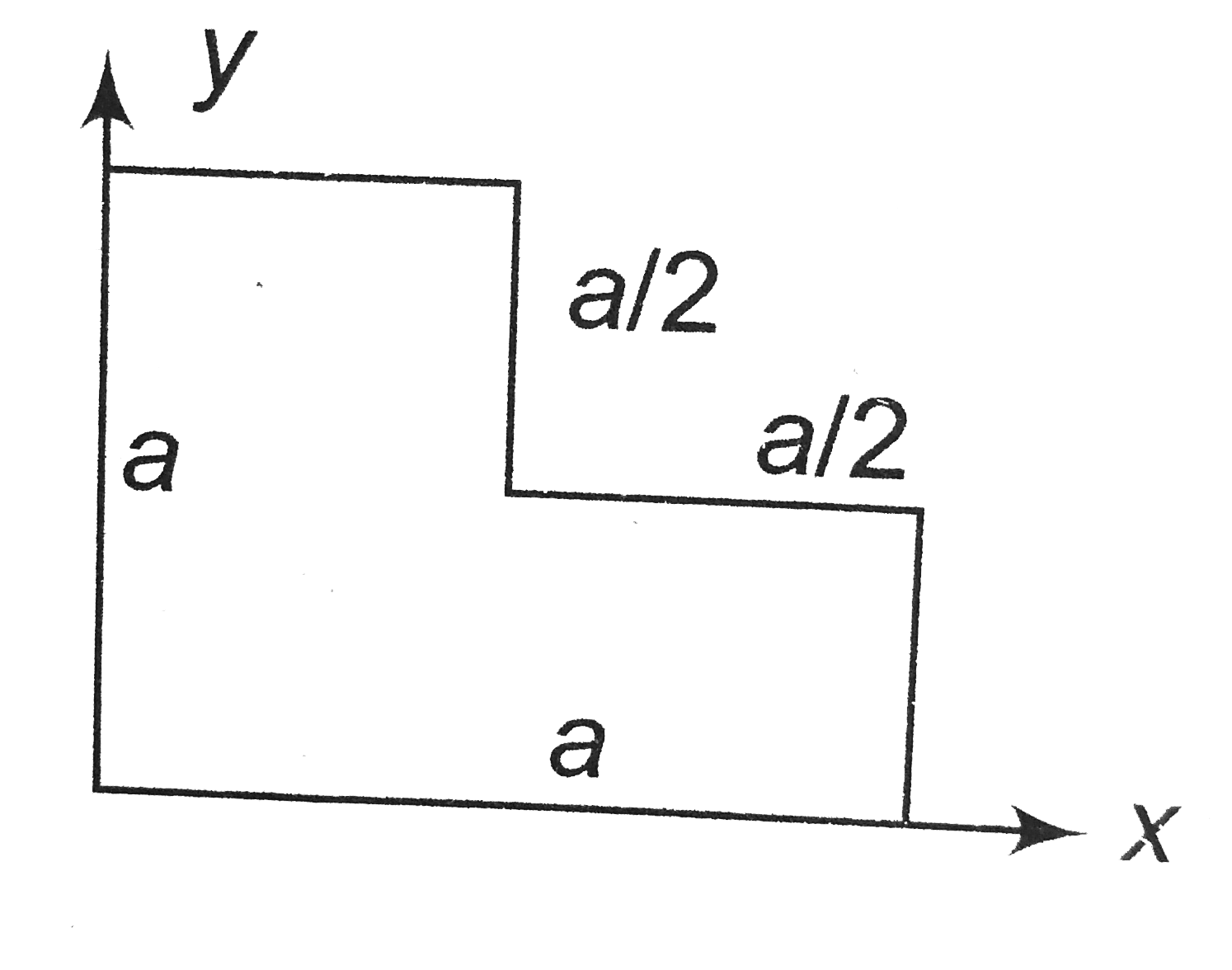 .A(512a,512a)B(712a,712a)C(14a,14a)D(13a,13a)
.A(512a,512a)B(712a,712a)C(14a,14a)D(13a,13a) - Question 2 - Select One
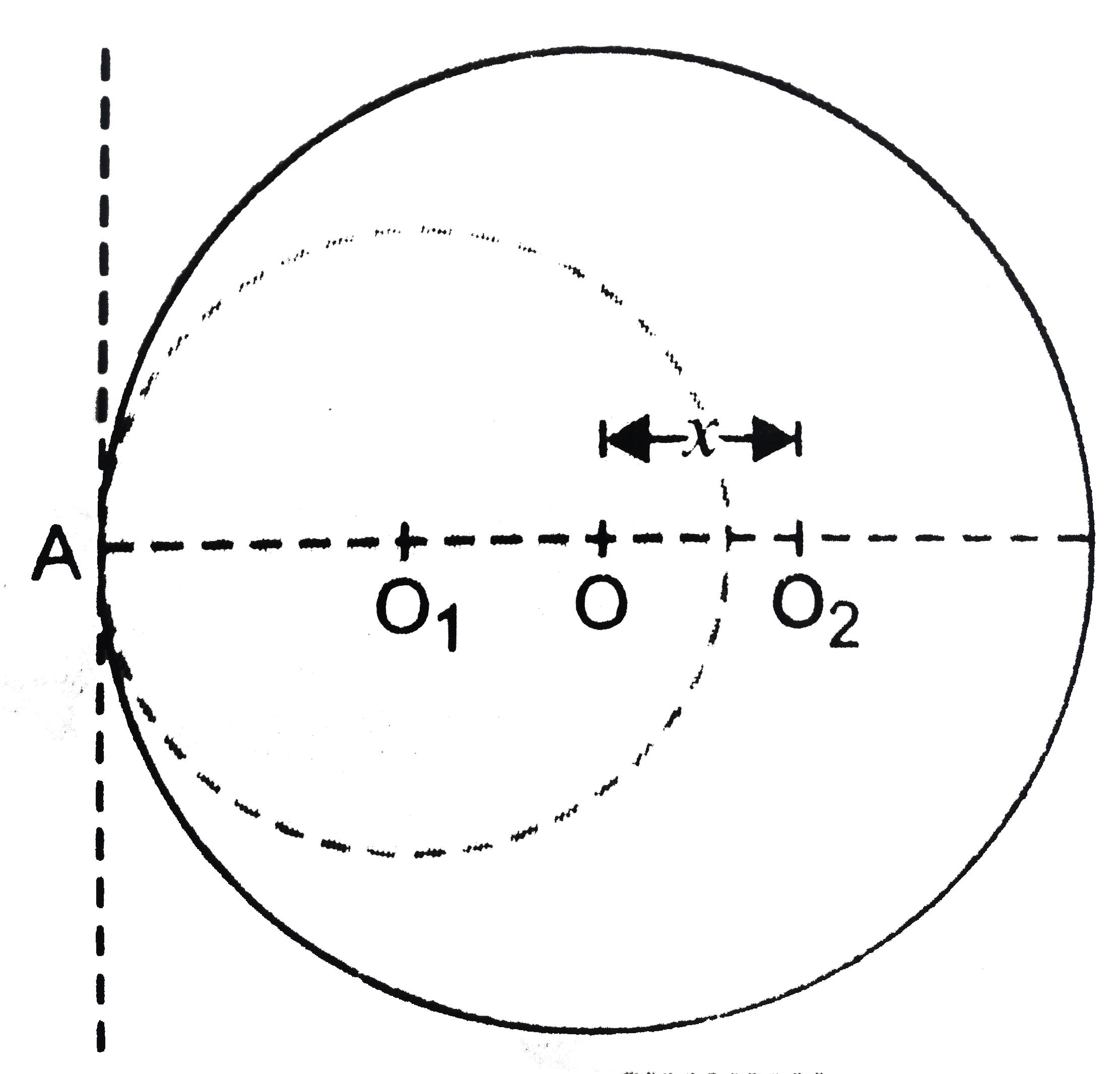
A square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is
 Aat O1Bat OC0.54 cm from O on the left hand sideDNone of the above
Aat O1Bat OC0.54 cm from O on the left hand sideDNone of the above - Question 3 - Select One
A square of side 2cm and uniform thickness is divided into four squares. The square portion A′AB′D is removed and the removed portion is placed over the portion DB′BC′. The new position of centre of mass is
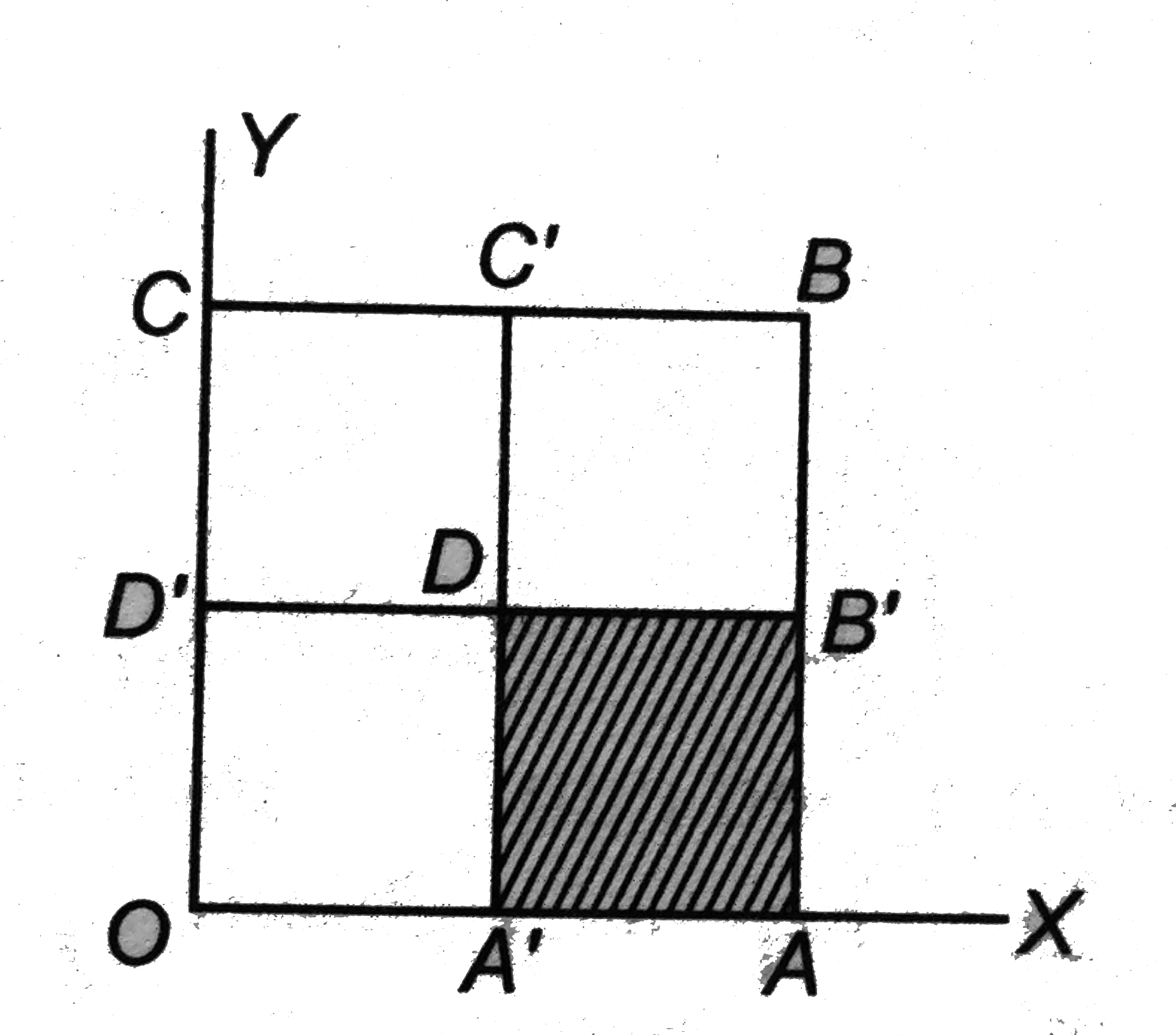 A(2cm,2cm)B(2cm,3cm)C(2cm,2.5cm)D(3cm,3cm)
A(2cm,2cm)B(2cm,3cm)C(2cm,2.5cm)D(3cm,3cm)
A square shaped hole of side l=a2 is carved out at a distance d=a2 from the centre 'O' of a uniform circular disk of radius a. If the distance of the centre of mass of the remaining portion from O is −ax value of X (to the nearest integer) is _________.
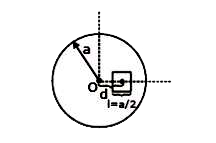 View Solution
View SolutionA circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.
 View Solution
View SolutionFrom a uniform square plate, one-fourth part is removed as shown. The centre of mass of remaining part will lie on
 View Solution
View SolutionFrom a square sheet of uniform density , a portion a removed shown shaded in fig. Find the centre of msas of the remaining portion is the side of the square is α
 View Solution
View SolutionFigure shows a square plate of uniform thickness and side length √2m. One fourth of the plate is removed as indicated. The distance of centre of mass of the remaining portion from the centre of the original square plate is
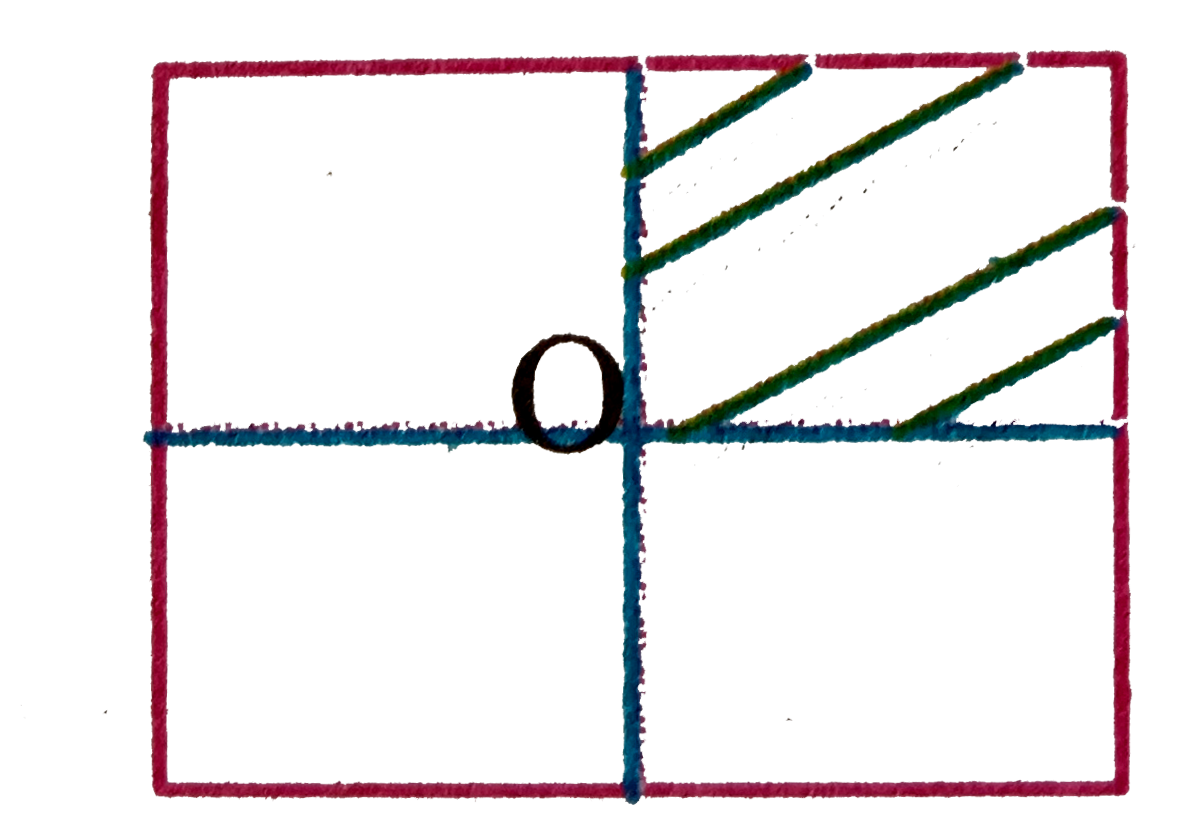 View Solution
View Solution

