A square shaped hole of side l=a2 is carved out at a distance d=a2 from the centre 'O' of a uniform circular disk of radius a. If the distance of the centre of mass of the remaining portion from O is −ax value of X (to the nearest integer) is _________.
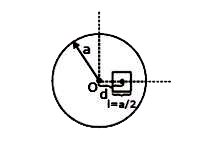
Xcm=πa2×0−a24×a2πa2−a24
=−a2(4π−1)=−a8π−2
X=(8π−2)=8×3.14−2
=23.12
Nearest Integer = 23
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The distance of centre of mass from O is
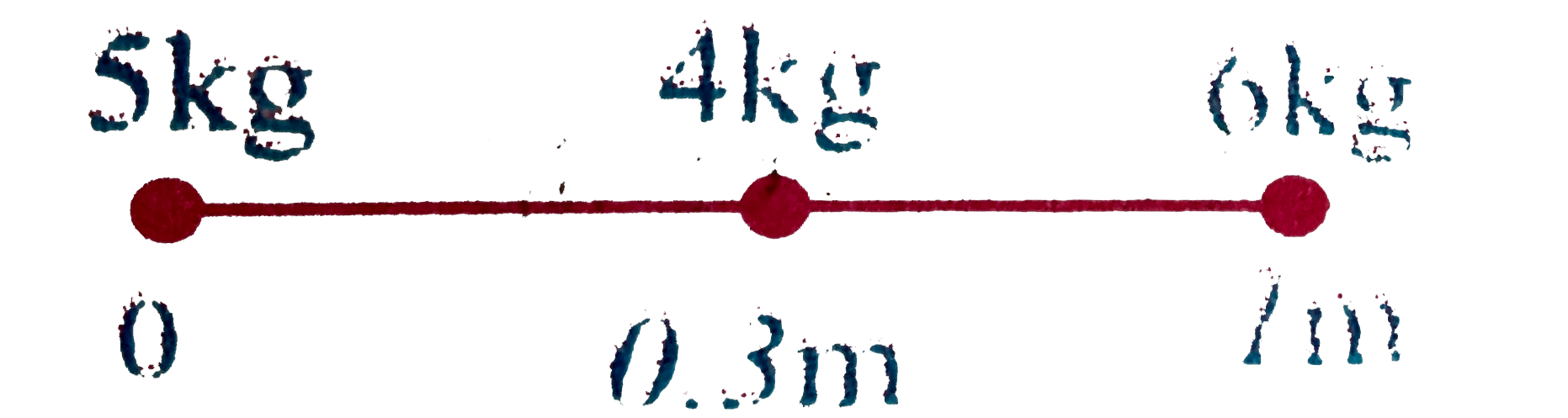 A0.21mB0.35mC0.42mD0.48m
A0.21mB0.35mC0.42mD0.48m - Question 2 - Select One
In the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
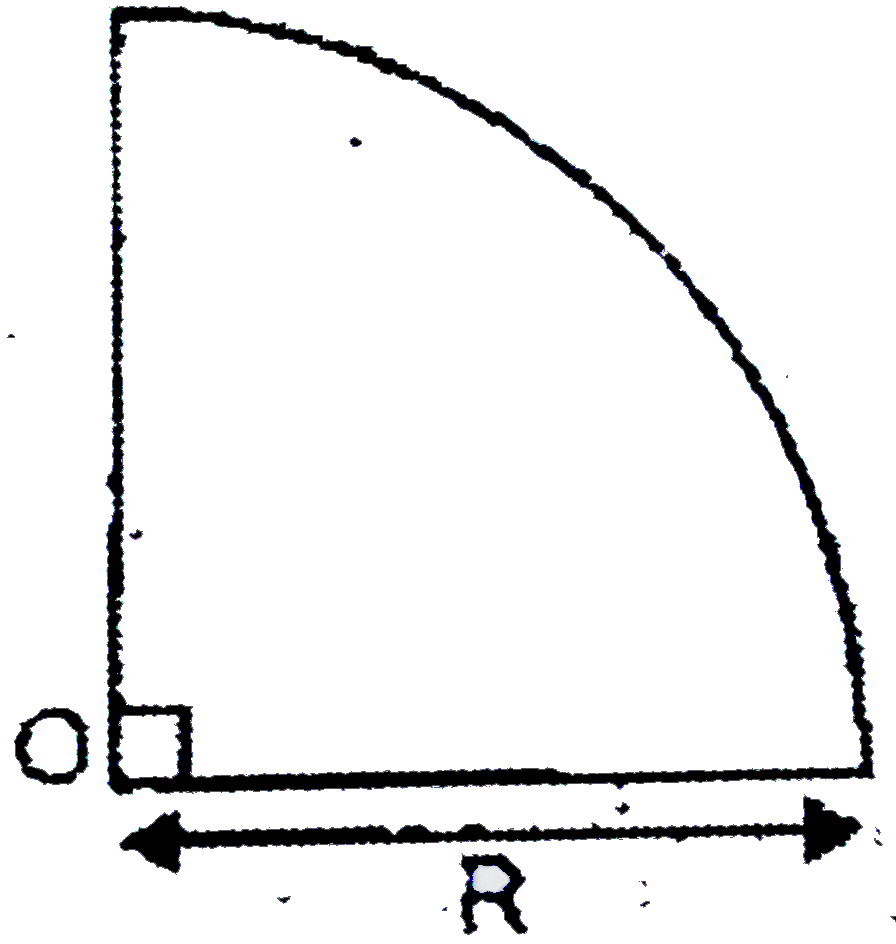 A4R3πB2r3πC√24R3πD√22R3π
A4R3πB2r3πC√24R3πD√22R3π - Question 3 - Select One
From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
AR4π−2BR2πCRπ−2DR2π−2
A disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion
 View Solution
View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is
 View Solution
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −
 View Solution
View SolutionIn the figure shown a hole of radius 2 cm is made in a semicircular disc of radius 6π at a distance 8 cm from the centre C of the disc. The distance of the centre of mass of this system from point C is :
 View Solution
View SolutionA square of side a2 is removed from a disc having radius a . Find centre of mass of remaing portion.
 View Solution
View Solution