An elastic ball of mass m falls from a height h on an Aluminium disc of area A floating in a mercury pool. If the collision is perfectly elastic, the momentum transferred to the disc is :
√2mgh
2√mgh
m√2gh
2m√2gh
The correct Answer is:D
To solve the problem of momentum transferred to the disc when an elastic ball of mass m falls from a height h and collides with an aluminum disc, we can follow these steps:
Step 1: Determine the velocity of the ball just before the collision
When the ball falls from a height h, we can use the equation of motion to find its velocity just before it hits the disc. The velocity v just before impact can be calculated using the formula:
v=√2gh
where g is the acceleration due to gravity.
Step 2: Understand the nature of the collision
Since the collision is perfectly elastic, both momentum and kinetic energy are conserved. In an elastic collision, the coefficient of restitution e is equal to 1.
Step 3: Apply conservation of momentum
Let:
- u1=√2gh (initial velocity of the ball)
- u2=0 (initial velocity of the disc, as it is floating)
Using the conservation of momentum for the elastic collision, we can express the final velocities after the collision:
mu1+Mu2=mv1+Mv2
where v1 and v2 are the final velocities of the ball and the disc, respectively. Since the disc is floating, we can assume its mass M is much larger than m, and thus the velocity of the disc after the collision will be very small.
Step 4: Use the coefficient of restitution
The coefficient of restitution for a perfectly elastic collision is given by:
e=v2−v1u1−u2
Substituting e=1:
1=v2−v1u1−0
This implies:
v2−v1=u1
Thus, we can express v2 in terms of v1:
v2=v1+u1
Step 5: Calculate the change in momentum
The change in momentum Δp transferred to the disc can be calculated as:
Δp=m(v1−u1)+M(v2−u2)
Since u2=0 and v1 will be negative after the collision (the ball rebounds), we can substitute:
Δp=m(−√2gh−√2gh)+Mv2
This simplifies to:
Δp=2m√2gh
Final Answer
Thus, the momentum transferred to the disc is:
Δp=2m√2gh
When the ball falls from a height h, we can use the equation of motion to find its velocity just before it hits the disc. The velocity v just before impact can be calculated using the formula:
v=√2gh
where g is the acceleration due to gravity.
Since the collision is perfectly elastic, both momentum and kinetic energy are conserved. In an elastic collision, the coefficient of restitution e is equal to 1.
Let:
- u1=√2gh (initial velocity of the ball)
- u2=0 (initial velocity of the disc, as it is floating)
mu1+Mu2=mv1+Mv2
where v1 and v2 are the final velocities of the ball and the disc, respectively. Since the disc is floating, we can assume its mass M is much larger than m, and thus the velocity of the disc after the collision will be very small.
The coefficient of restitution for a perfectly elastic collision is given by:
e=v2−v1u1−u2
Substituting e=1:
1=v2−v1u1−0
This implies:
v2−v1=u1
Thus, we can express v2 in terms of v1:
v2=v1+u1
The change in momentum Δp transferred to the disc can be calculated as:
Δp=m(v1−u1)+M(v2−u2)
Since u2=0 and v1 will be negative after the collision (the ball rebounds), we can substitute:
Δp=m(−√2gh−√2gh)+Mv2
This simplifies to:
Δp=2m√2gh
Thus, the momentum transferred to the disc is:
Δp=2m√2gh
Similar Questions
A ball is dropped from height 'h' as shown.The collision is perfectly inelastic. Select the correct alternative (s)
View SolutionTwo ball bearings of mass m each moving in opposite directions with same speed v collide head on with each other. If the collision is perfectly elastic, what will be the outcome of the collision ?
View Solution
Knowledge Check
A molecule of mass 'm' collide with a wall of container in normal direction with a velocity c. if the collision is perfectly elastic, then the change in momentum of the molcules is
AzeroBmcC+2mcD−2mcA ball is allowed to fall from a height of 8cm, if the ball is perfectly elastic, how much it rise after rebound-
A8 cmB1 cmC0.5 cmD0Two balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
Aπ4Bπ3Cπ6Dπ2
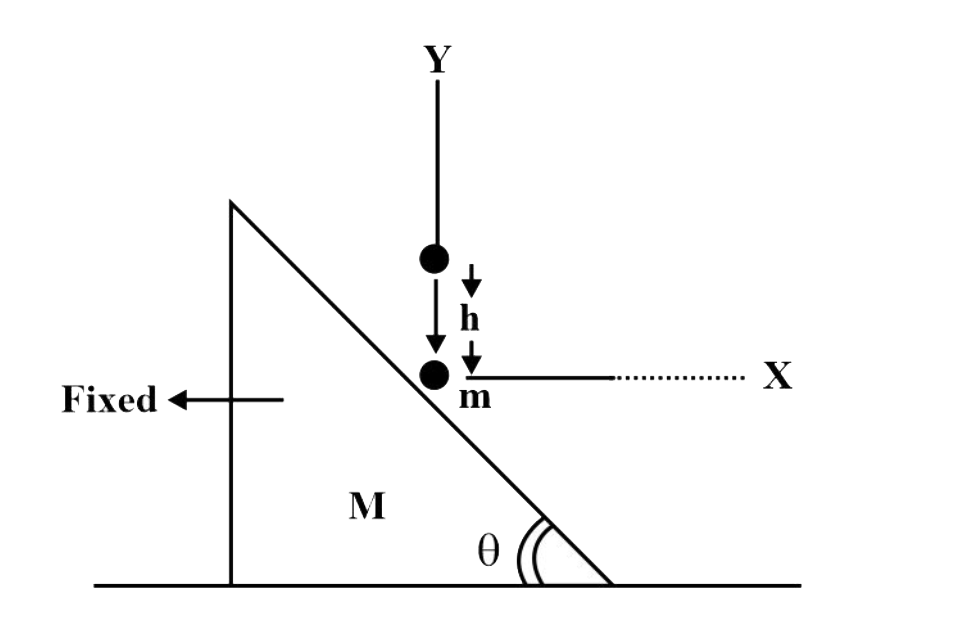
A ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is component of the velocity of the block is √2gh , then θ is
View SolutionA steel ball of mass 0.5 kg is dropped from a height of 4 m on to a horizontal heavy steel slab. The collision is elastic and the ball rebounds to its original height.
If the ball is in contact with the slab for 0.002 s, find the average reaction force on the ball during impact.
View SolutionTwo balls each of mass 2kg (one at rest) undergo oblique collision is perfectly elastic, then the angle between their velocities after collision is
View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View SolutionA body of mass 'm' moving with certain velocity collides with another identical body at rest. If the collision is perfectly elastic and after the collision both the bodies moves
View Solution
