A particle of mass ‘m’ is moving with speed ‘2v’ and collides with a mass ‘2m’ moving with speed ‘v’ in the same direction. After collision, the first mass is stopped completely while the second one splits into two particles each of mass ‘m’, which move at angle 45∘ with respect to the original direction. The speed of each of the moving particle will be:
2√2v
v/(2√2)
√2v
v/√2
The correct Answer is:A
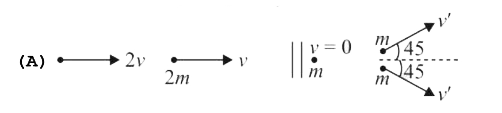
Linear momentum conservation
m2v+2mv=m×0+mv'√2×2,v'=2√2v.
Similar Questions
A particle of mass m moving with velocity 2v collides with another particle of mass 3m moving with velocity v in the same direction.If it is perfect inelastic collision,the loss of kinetic energy of the system is
View SolutionA particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m1 moving with velocity v collides with a mass m2 at rest, then they get embedded. Just after collision, velocity of the system
AincreasesBdecreasesCremains constantDbecomes zero - Question 2 - Select One
A particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
Av3B−v3C2v3D−2v3 - Question 3 - Select One
A particle of mass m is moving along the x-axis with speed v when It collides with a particle of mass 2m initially at rest. After the collision, the first particle has come to rest and the second particle has split into two equal-mass pieces that are shown in the figure. Which of the following statements correctly describes the speeds of the two places? (θ>0)
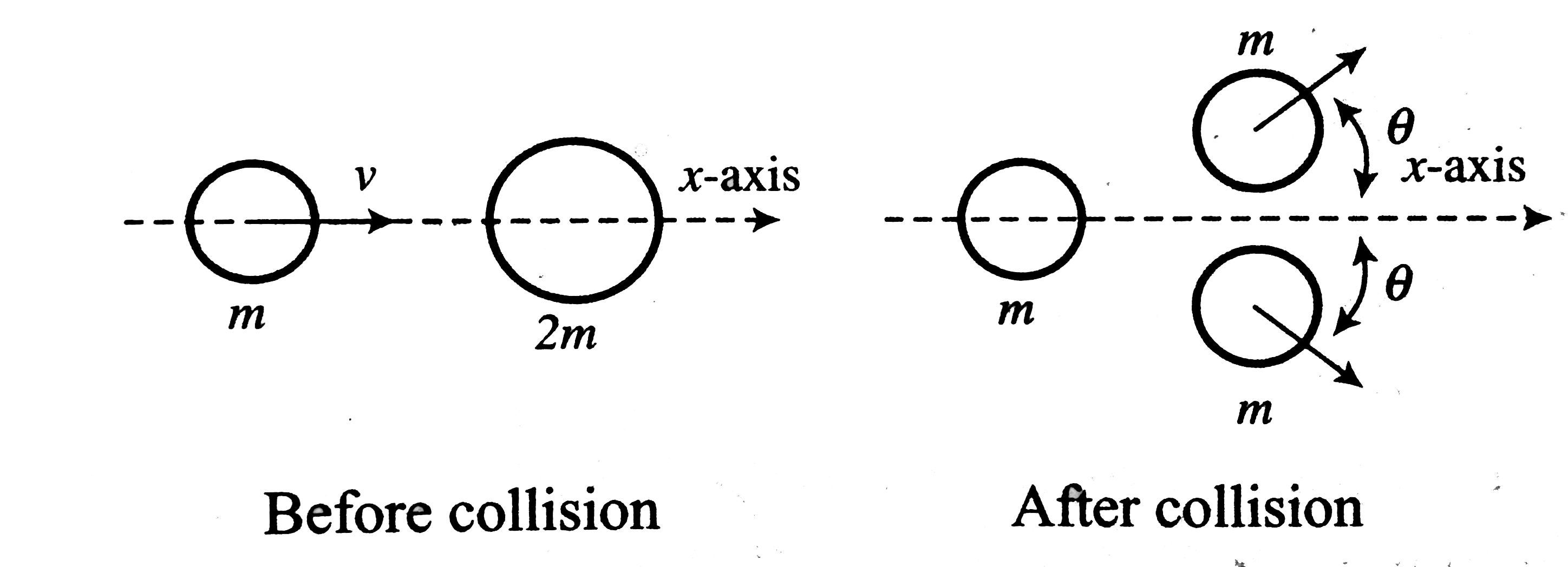 Aeach piece moves with speed v.Beach piece moves with speed v/2.Cone of the pieces moves with speed v/2, the other moves with speed greater than v/2.Deach piece moves with speed greater than v/2.
Aeach piece moves with speed v.Beach piece moves with speed v/2.Cone of the pieces moves with speed v/2, the other moves with speed greater than v/2.Deach piece moves with speed greater than v/2.
A particle of mass m moving on a smooth surface with velocity 10m/s strikes another particle of mass 2m moving with 5m/s in the same direction . If the collision is elastic and head - on , find velocities of particles after the collision.
View SolutionA particle of mass 0.1kg moving with an initial speed v collides with another particle of same mass kept at rest. If after collision total energy becomes 0.2J . Then
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to:
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
View Solution
