A small compass needle of magnetic moment ‘M’ and moment of inertial ‘I’ is free to oscillate in a magnetic field ‘B’. It is slightly disturbed from its equilibrium position and then released. Show that it executes simple harmonic motion. Hence, write the expression for its time period.
To show that a small compass needle of magnetic moment M and moment of inertia I executes simple harmonic motion (SHM) when slightly disturbed in a magnetic field B, we can follow these steps:
Step 1: Understanding the System
When the compass needle is in equilibrium, it aligns itself with the magnetic field. If it is slightly disturbed by an angle θ, it experiences a torque due to the magnetic field.
Hint: Consider the forces acting on the compass needle when it is displaced from equilibrium.
Step 2: Torque Acting on the Needle
The torque τ acting on the compass needle can be expressed as:
τ=−MBsinθ
where M is the magnetic moment and B is the magnetic field strength. The negative sign indicates that the torque acts in the opposite direction to the displacement.
Hint: Recall that torque is the product of the magnetic moment and the magnetic field.
Step 3: Relating Torque to Angular Acceleration
According to Newton's second law for rotation, the torque is also related to the angular acceleration α and moment of inertia I:
τ=Iα
Substituting the expression for torque, we have:
−MBsinθ=Id2θdt2
Hint: Remember that angular acceleration is the second derivative of angular displacement with respect to time.
Step 4: Small Angle Approximation
For small angles θ, we can use the approximation sinθ≈θ (in radians). Thus, the equation simplifies to:
−MBθ=Id2θdt2
Hint: This approximation is valid for small displacements and is crucial for deriving SHM.
Step 5: Rearranging the Equation
Rearranging the equation gives:
d2θdt2+MBIθ=0
This is the standard form of the equation for simple harmonic motion, where:
ω2=MBI
Hint: Identify the form of the equation that indicates SHM.
Step 6: Time Period of the Oscillation
The time period T of the oscillation can be derived from the relationship between angular frequency ω and time period:
T=2π√IMB
Hint: Remember the relationship between frequency, angular frequency, and time period.
Final Expression
Thus, the time period T of the simple harmonic motion of the compass needle is given by:
T=2π√IMB
Summary
In conclusion, we have shown that a small compass needle executes simple harmonic motion when slightly disturbed in a magnetic field and derived the expression for its time period as T=2π√IMB.
When the compass needle is in equilibrium, it aligns itself with the magnetic field. If it is slightly disturbed by an angle θ, it experiences a torque due to the magnetic field.
The torque τ acting on the compass needle can be expressed as:
τ=−MBsinθ
where M is the magnetic moment and B is the magnetic field strength. The negative sign indicates that the torque acts in the opposite direction to the displacement.
According to Newton's second law for rotation, the torque is also related to the angular acceleration α and moment of inertia I:
τ=Iα
Substituting the expression for torque, we have:
−MBsinθ=Id2θdt2
For small angles θ, we can use the approximation sinθ≈θ (in radians). Thus, the equation simplifies to:
−MBθ=Id2θdt2
Rearranging the equation gives:
d2θdt2+MBIθ=0
This is the standard form of the equation for simple harmonic motion, where:
ω2=MBI
The time period T of the oscillation can be derived from the relationship between angular frequency ω and time period:
T=2π√IMB
Thus, the time period T of the simple harmonic motion of the compass needle is given by:
T=2π√IMB
In conclusion, we have shown that a small compass needle executes simple harmonic motion when slightly disturbed in a magnetic field and derived the expression for its time period as T=2π√IMB.
Similar Questions
A small compass needle of magnetic moment 'm' and moment of inertia 'l' is free to oscillate in a magnetic field 'B'. It is slightly disturbed from its equilibrium position and then released. Show that it executes simple harmonic motion. Hence, write the expression for its time period.
View Solution(a) A small compass needle of magnetic moment 'm' is free to turn about an axis perpendicular to the direction of uniform magnetic field 'B'. The moment of inertia of the needle about the axis is 'I'. The needle is slightly disturbed from its stable position and then released. Prove that it executes simple harmonic motion. Hence, deduce the expression for its time period .
(b) A compass needle , free to turn in a vertical orients itself with its axis vertical at a certain place on the earth . Find out the values of (i) horizontal component of earth's magnetic field and (ii) angle of dip at the place.
View Solution
Knowledge Check
A magnet of magnetic moment M and having moment of inertia I , is suspended to orient freely in the horizontal plane under the influence of earth's magnetic field . If it is slightly disturbed , the time period is given by
A2π√IMBHB2π√MBHIC12π√IMBHD12π√MBHIA magnetic needle of magnetic moment 6⋅7×10−2Am2 and moment of inertia 7⋅5×10−6kgm2 is performing simple harmonic oscillations in a magnetic field of 0⋅01T. Time taken for 10 complete oscillation is
A6⋅98sB8⋅76sC6⋅65sD8⋅89sRead the following passage on the basis of your understanding of the following paragraph and the related studied concepts:
A freely suspended bar magnet capable of rotation in a horizontal plane in its equilibrium state, rests in the direction of earth's magnetic field at the place. If the magnet is slightly rotated from its equilibrium direction and then released, it executes angular oscillations of period T given as per relation
T=2π√ImBH
Here I moment of inertia of bar magnet about its oscillation axis, magnetic moment of bar magnet and BH horizontal component of earth's magnetic field at the place.
An oscillation magnetometer is designed on this principle and is employed to compare magnetic moments of magnets and for determining earth's magnetic field at a place.
The oscillation period of a given magnetic needle is 5 s at place A and 6 s at place B. The ratio of horizontal components of earth's magnetic field at A and B isA56B3625C125D65
A small compass needle of magnetic moment M is free to turn about an axis perpendicular to the direction of uniform magnetic field B. The moment of inertia of the needle about the axis is I. The needle is slightly displaced from its stable position and then released. Prove that it executes simple harmonic motion. Hence deduce the expression for its time period.
View Solution(a)Derive the expression for the torque on a rectangular current carrying loop suspended in a uniform magnetic field.
(b)A proton and a deuteron having equal momenta enter in a a region of a uniform magnetic field at right angle to the direction of a the field.Depict their trajectories in the field.
OR
(a)A small compass needle of magnetic moment m is free to turn about an axis perpendicular to the direction of unifrom magnetic field B.The moment of inertia of the needle about the axis is I.The needle is slightly disturbed form its stable position and then released.Prove that it executes simple harmonic motion.Hence deduce the expression for its time period.
(b) A compass needle, free to turn in a vertical plane orients inself with its axis vertical at a certain place on the earth.Find out the values of (i)horizontal component of earth's magnetic field and (ii) angle of dip at the place.
View SolutionShow that for a small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression of its time period.
View SolutionA magnetic dipole of magnetic moment M is suspended by a string in a uniform horizontal magnetic field as showo in figure. If in horizontal plane this dipole is slightly tilted and released, show that it will execute simple harmonic motion and find its oscillation period. Consider the dipole as a uniform rod of mass m and length I.
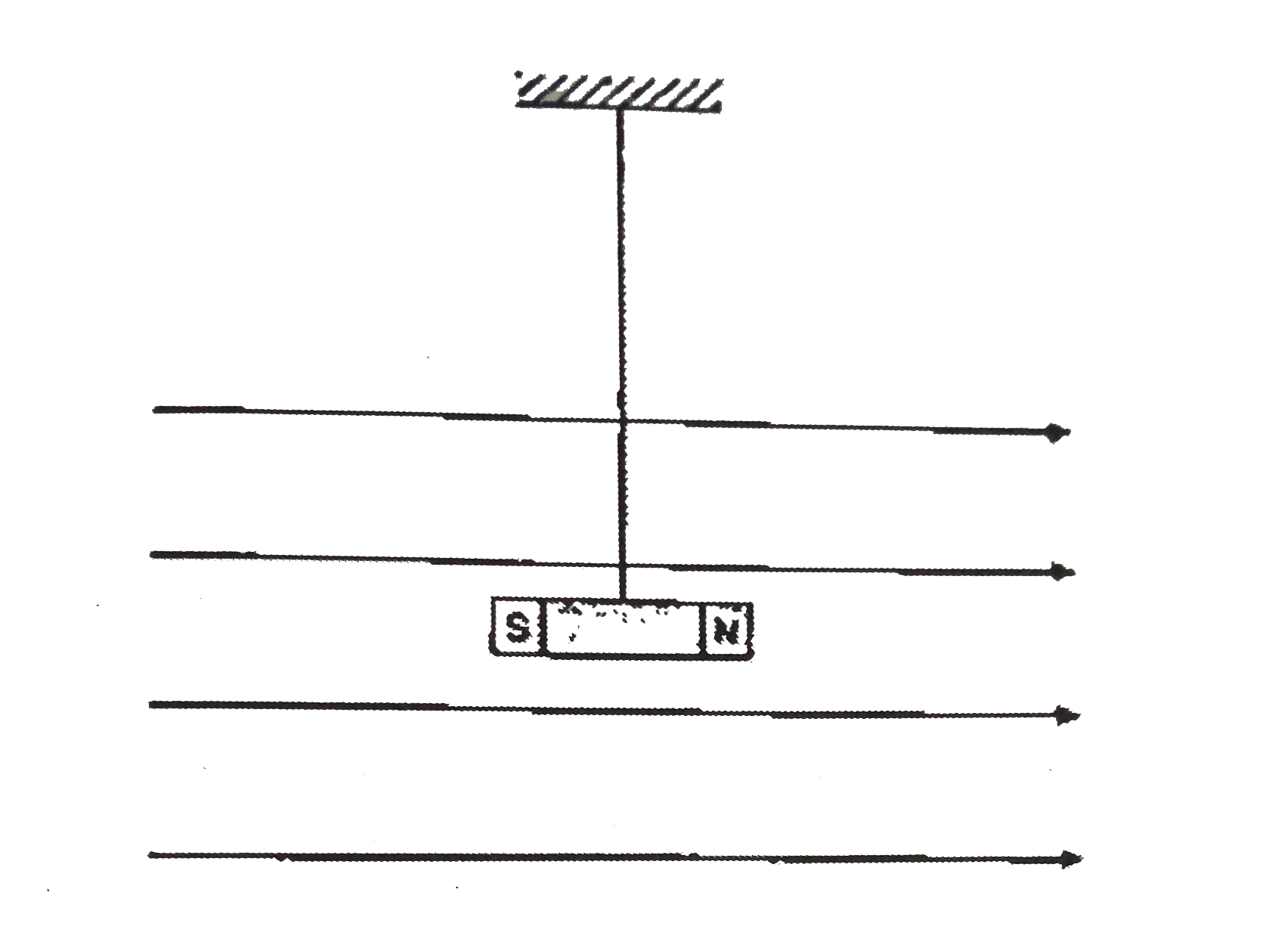
View SolutionRead the following passage on the basis of your understanding of the following paragraph and the related studied concepts:
A freely suspended bar magnet capable of rotation in a horizontal plane in its equilibrium state, rests in the direction of earth's magnetic field at the place. If the magnet is slightly rotated from its equilibrium direction and then released, it executes angular oscillations of period T given as per relation
T=2π√ImBH
Here I moment of inertia of bar magnet about its oscillation axis, magnetic moment of bar magnet and BH horizontal component of earth's magnetic field at the place.
An oscillation magnetometer is designed on this principle and is employed to compare magnetic moments of magnets and for determining earth's magnetic field at a place.
Two bar magnets A and B of same configuration and mass have oscillation periods of 2s and 2.5 s respectively at a given place. The ratio of magnetic moments of A and B is
View Solution
