Question

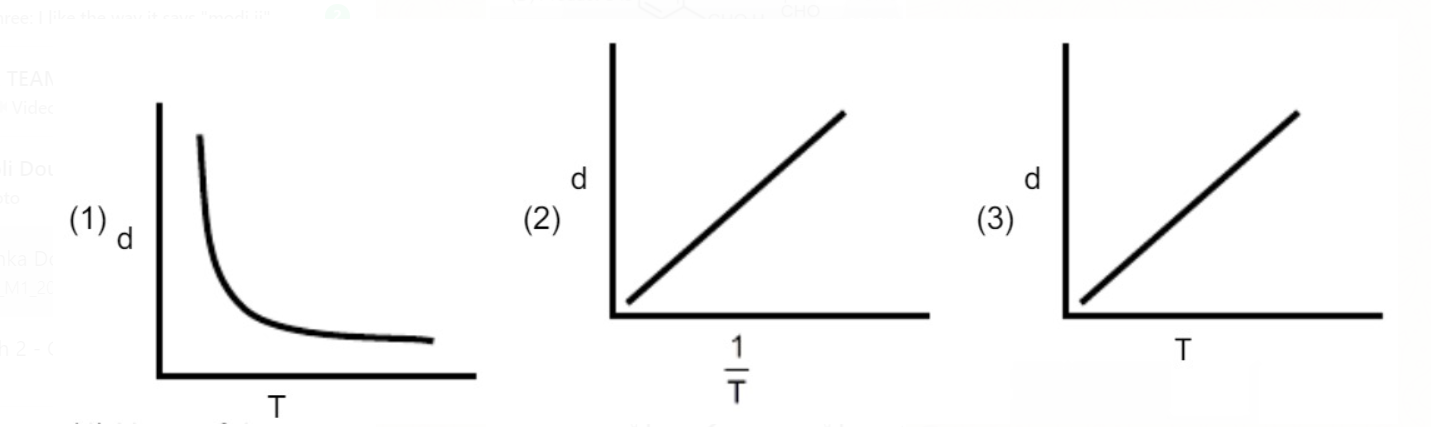
For an ideal gas which of the following graphs will not be straight line when all the other variables are held constant?

Options

A. P vs T
B. V vs T
C. `P vs (1)/(V)`
D. n vs T

Answer

D

Explanation

To solve the question of which graph will not be a straight line for an ideal gas when all other variables are held constant, we can analyze each option based on the ideal gas law, which is given by the equation:

$$PV=nRT$$

Where:
- $$P$$ = Pressure
- $$V$$ = Volume
- $$n$$ = Number of moles
- $$R$$ = Ideal gas constant
- $$T$$ = Temperature

Now, let’s evaluate each option step by step:

Step 1: Analyze the first option - Graph of \( P \) vs \( T \)
- If we hold \( V \) and \( n \) constant, from the ideal gas equation, we can express \( P \) in terms of \( T \):
\( P = \frac{nRT}{V} \)
- This shows that \( P \) is directly proportional to \( T \). Therefore, the graph of \( P \) vs \( T \) will be a straight line.

Step 2: Analyze the second option - Graph of \( V \) vs \( T \)
- Holding \( P \) and \( n \) constant, we can express \( V \) in terms of \( T \):
\( V = \frac{nRT}{P} \)
- This indicates that \( V \) is directly proportional to \( T \). Thus, the graph of \( V \) vs \( T \) will also be a straight line.

Step 3: Analyze the third option - Graph of \( P \) vs \( \frac{1}{V} \)
- Holding \( n \) and \( T \) constant, we can express \( P \) in terms of \( \frac{1}{V} \):
\( P = \frac{nRT}{V} \)
- This shows that \( P \) is directly proportional to \( \frac{1}{V} \). Therefore, the graph of \( P \) vs \( \frac{1}{V} \) will also be a straight line.

Step 4: Analyze the fourth option - Graph of \( T \) vs \( n \)
- Holding \( P \) and \( V \) constant, we can express \( T \) in terms of \( n \):
\( PV = nRT \implies T = \frac{PV}{nR} \)
- Here, \( T \) is inversely proportional to \( n \) (as \( n \) increases, \( T \) decreases). Therefore, the graph of \( T \) vs \( n \) will not be a straight line; it will be a hyperbola.

Conclusion
The graph that will not be a straight line is the fourth option, which is the graph of \( T \) vs \( n \).

Final Answer
The fourth option (Graph of \( T \) vs \( n \)) will not be a straight line.

---