The displacement of a particle is given by x=(t−2)2 where x is in meter and t in second. The distance covered by the particle in first 3 seconds is
4 m
8 m
12 m
16 m
The correct Answer is:D
Given , x=(t−2)2
Velocity, v=dxdt=ddt(t−2)2=2(t−2)m/s
Acceleration, a=dvdt=ddt[2(t−2)]
=2[1−0]=2m/s2
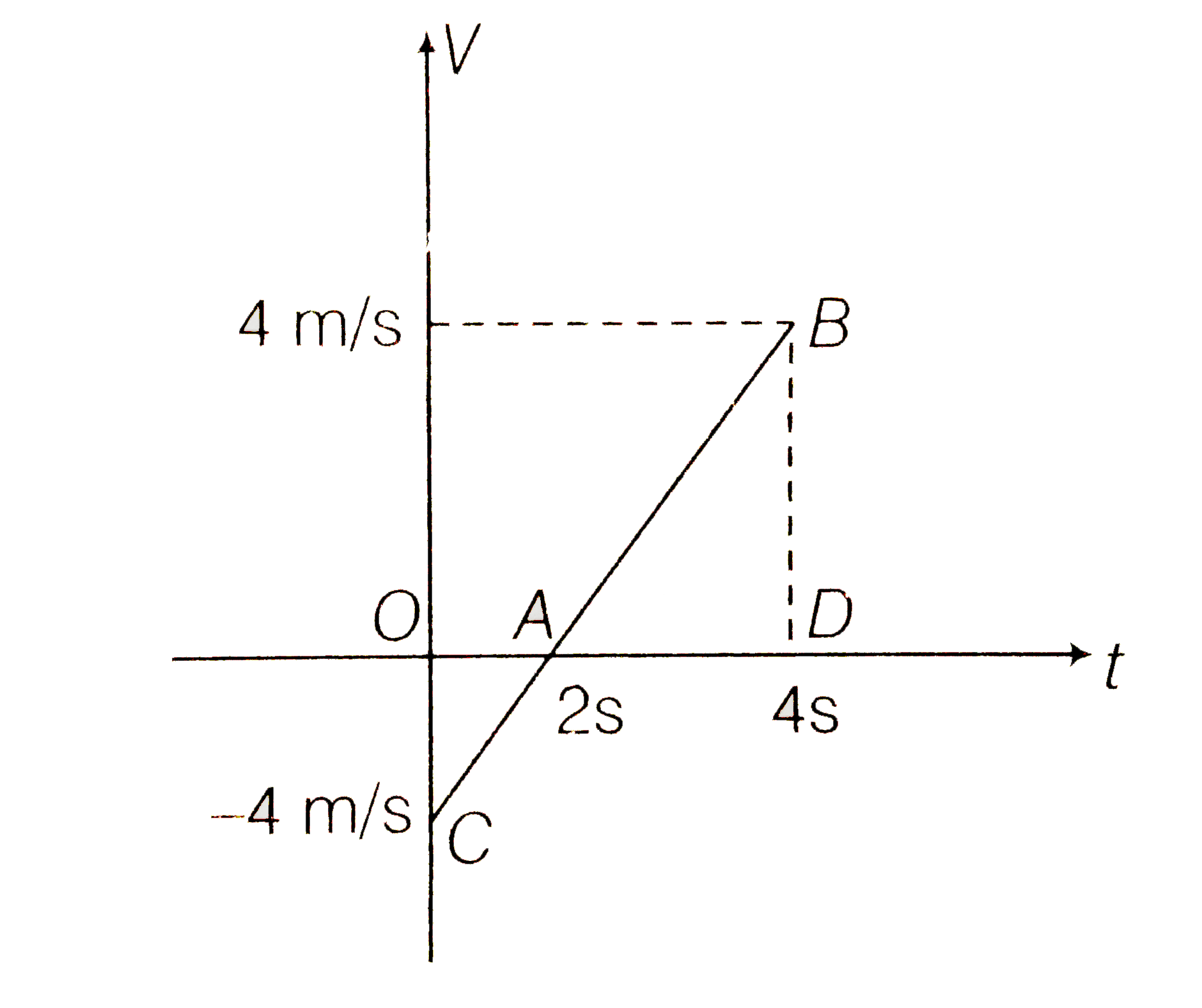
When t=0,v=−4m/s
t=2s,v=0m/s
t=4s,v=4m/s
v−t graph is shown in adjacent diagram,
Distance travelled = area of the graph
= area of OAC+ area ABD
=4×22+12×2×4=8m
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - NCERT EXEMPLARCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Multiple Choice Question (More Than One Qns)
6 Videos
- MOTION IN A STRAIGHT LINE BOOK - NCERT EXEMPLARCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Very Short Answer Type Qns
14 Videos
- MOTION IN A PLANEBOOK - NCERT EXEMPLARCHAPTER - MOTION IN A PLANEEXERCISE - Multiple Choice Questions
37 Videos
- OSCILLATIONSBOOK - NCERT EXEMPLARCHAPTER - OSCILLATIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (MCQs)
40 Videos
Similar Questions
The x -coordinate of a particle moving along x -axis varies with time as x=6-4t+t^(2), where x in meter and t in second then distance covered by the particle in first 3 seconds is
View SolutionThe displacement of a particle is given by y=(6t2+3t+4)m, where t is in seconds. Calculate the instantaneous speed of the particle.
View Solution
Knowledge Check
The displacement of a particle is moving by x=(t−2)2 where x is in metres and t in second. The distance covered by the particle in first 4 seconds is.
A4mB8mC12 mD16 mThe displacement of a particle is moving by x=(t−2)2 where x is in metres and t in second. The distance covered by the particle in first 4 seconds is.
A4 mB8 mC12 mD16 mThe position x of a particle varies with time t as x=6+12t−2t2 where x is in metre and t is in seconds. The distance travelled by the particle in first five seconds is
A16 mB26 mC10 mD36 m
The displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionUnder the action of a force, a 2kg body moves such that its position x as a function of time is given by x=t33 where x is in meter and t in second. The work done by the force in the first two seconds is .
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The particle
View SolutionA force acts on a 3.0 gm particle in such a way that the position of the particle as a function of time is given by x=3t−4t2+t3, where xx is in metres and t is in seconds. The work done during the first 4 seconds is
View SolutionA force acts on a 3.0 gm particle in such a way that the position of the particle as a function of time is given by x=3t−4t2+t3, where xx is in metres and t is in seconds. The work done during the first 4 seconds is
View Solution
