A block of mass 1kg is pushed up a surface inclined to horizontal at an angle of 30∘ by a force of 10N parallel to the inclined surface [figure]. The coefficient of friction between block and the incline is 0.1. If the block is pushed up by 10 m along the incline, calculate
(a) work done against gravity
(b) work done against force of friction
(c) increase in potential energy
(d) increase in kinetic energy
(e) work done by applied force.
![A block of mass 1kg is pushed up a surface inclined to horizontal at an angle of 30^(@) by a force of 10N parallel to the inclined surface [figure]. The coefficient of friction between block and the incline is 0.1. If the block is pushed up by 10 m along the incline, calculate (a) work done against gravity (b) work done against force of friction (c) increase in potential energy (d) increase in kinetic energy (e) work done by applied force.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/PR_XI_VOL1_CH04_SO1_300_Q01.png)
Consider the adjacent digraam the block is pushed up by applyin a force F.
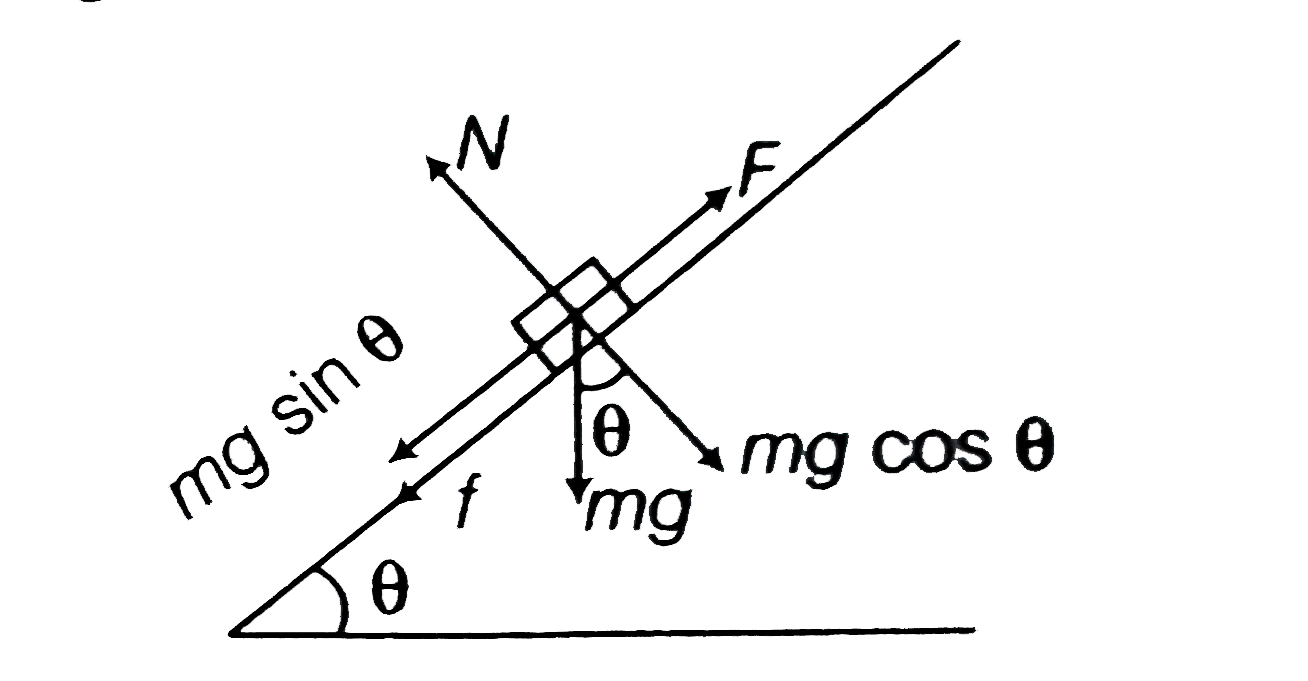
Normal reaction(N) and frictionless force(f) is shown
Given mass=m=1kg, θ=30∘
F=10N,μ,=0.1 and S=distance moved by the block along th inclined plane=10m
(a) Work done against gravity=Increase in PE of the block
=mg×Vertical distance travelled
=mg×s(sinθ)=mg×s(sinθ)=(mgs)sinθ
=1×10×10×sin30∘=50J (∴g≤10m/s2)
(b) Work done against friction
wf=f×s=μN×s=μmgcosθθ×5
=0.1×1×10×cos30∘×10
=1×10×10×sin30∘×10
(c ) Increase in PE=mghmg(ssinθ)
=1×10×10×sin30∘
100×12=50J
(d) By work energy theorem, we know that work done by all the foreces=change in KE
(W)=ΔK
Δk=Wg+Wf+Wf
=−mgh−fs+FS
−50−8.66+10×10
=50−8.66=41.34J
(e) Work done by applied force, F=FS
=(10)(10)=100J
(a) As ball 1 is rolling down without slipping there is no dissipation of energy hence, total mechanical energy is conserved. Ball 3 is having negligible friction hence, there is no loss of energy.
(b) Ball 1 acquire rotational energy, ball 2 loses energy by friction, They cannot cross at C. Ball 3 can cross over.
(c ) Ball 1,2 turn back before C. Because of loss of energy, ball 2 cannot reach back to A. Ball 1 has a rotational motion in "wrong" sense when it reaches B. It cannot roll back to A, because of kinetic friction.
Topper's Solved these Questions
Similar Questions
A block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal . Calculate the acceleration of the block . The coefficient of friction between the block and surface is 0⋅6 ( Take g = 10m/s2)
View Solution
Knowledge Check
A block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of 30∘ by a force of 10 N parallel to the inclined surface as shown in the figure.
The coefficient of friction between block and the incline is 0.1. If the block is pushed up by 10 m along the incline, then the work against gravity is (Take g=10ms−2)
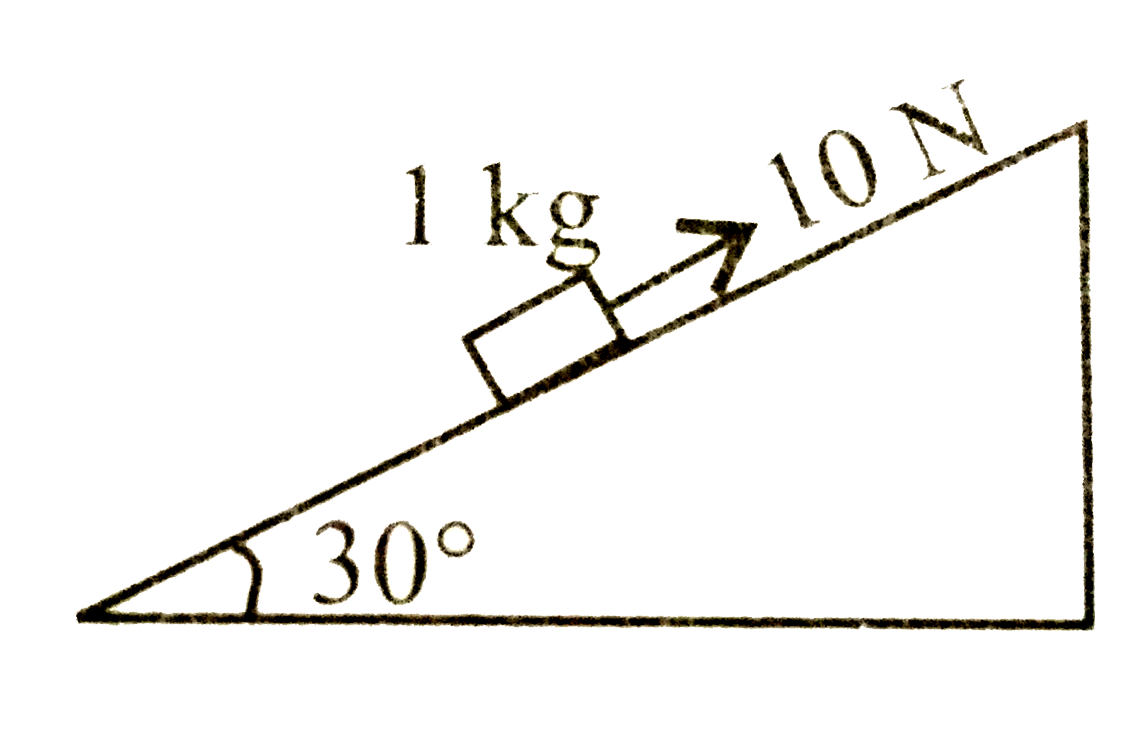 A10 JB50 JC100 JD150 J
A10 JB50 JC100 JD150 JIn the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5NA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
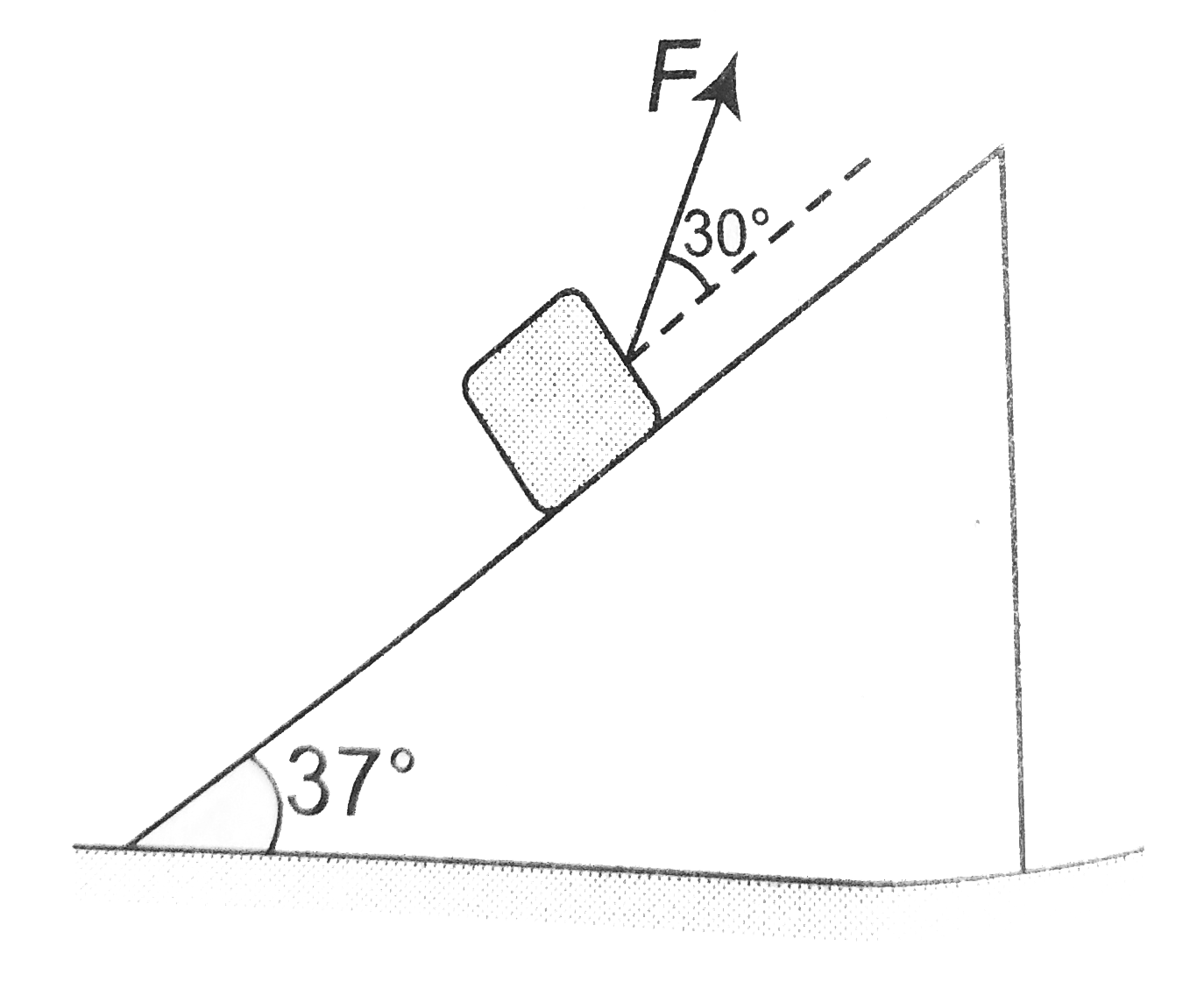 Astatic in nature in the direction up the plane and have the value 30.2NBstatic in nature in the direction down the plane and have the value 30.2NCkinetic in nature in the direction up the plane and have the value 30.2NDNone of these
Astatic in nature in the direction up the plane and have the value 30.2NBstatic in nature in the direction down the plane and have the value 30.2NCkinetic in nature in the direction up the plane and have the value 30.2NDNone of these
A block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View SolutionA block of mass 0.5 kg has an initial velocity of 10ms−1 down an inclined plane of angle 30∘, the coefficient of friction between the block and the inclined surface is 0.2. The velocity of the block after it travels a distance of 10 m is

View SolutionA block of mass 2kg is pushed down an inclined plane of angle 37∘ above horizontal with a force parallel to inclined plane. The coefficient of friction is (3)/(4). The block moves 10m in 2 seconds starting form rest. The magnitude of the force is
View SolutionA block of mass 10kg is pushed up on a smooth incline plane of inclination 30∘, so that it has acceleration 2m/s2. The applied force is
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View Solution
