A uniform cube of mass $m$ and side a is placed on a frictionless horizontal surface. A vertical force $F$ is applied to the edge as shown in Fig. Match the following (most appropriate choice) :
(a) $m g / 4 < F < m g / 2$ (i) Cube will move up.
(b) $F > m g / 2$ (ii) Cube will not exhibit motion.
(c ) $F > m g$ (iii) Cube will begin to rotate and slip at $A$ .
(d) $F = m g / 4$ (iv) Normal reaction effectively at $a / 3$ from A, no motion.

Video Solution

Text Solution

Verified by Experts

Consider the below diagram
Moment of the force F about point A $τ_{1} = F \times a$ (anti - clockwise )
moment of weight mg of the cube about point A ,
$τ_{2} = m g \times \frac{a}{2}$ (clock wise )

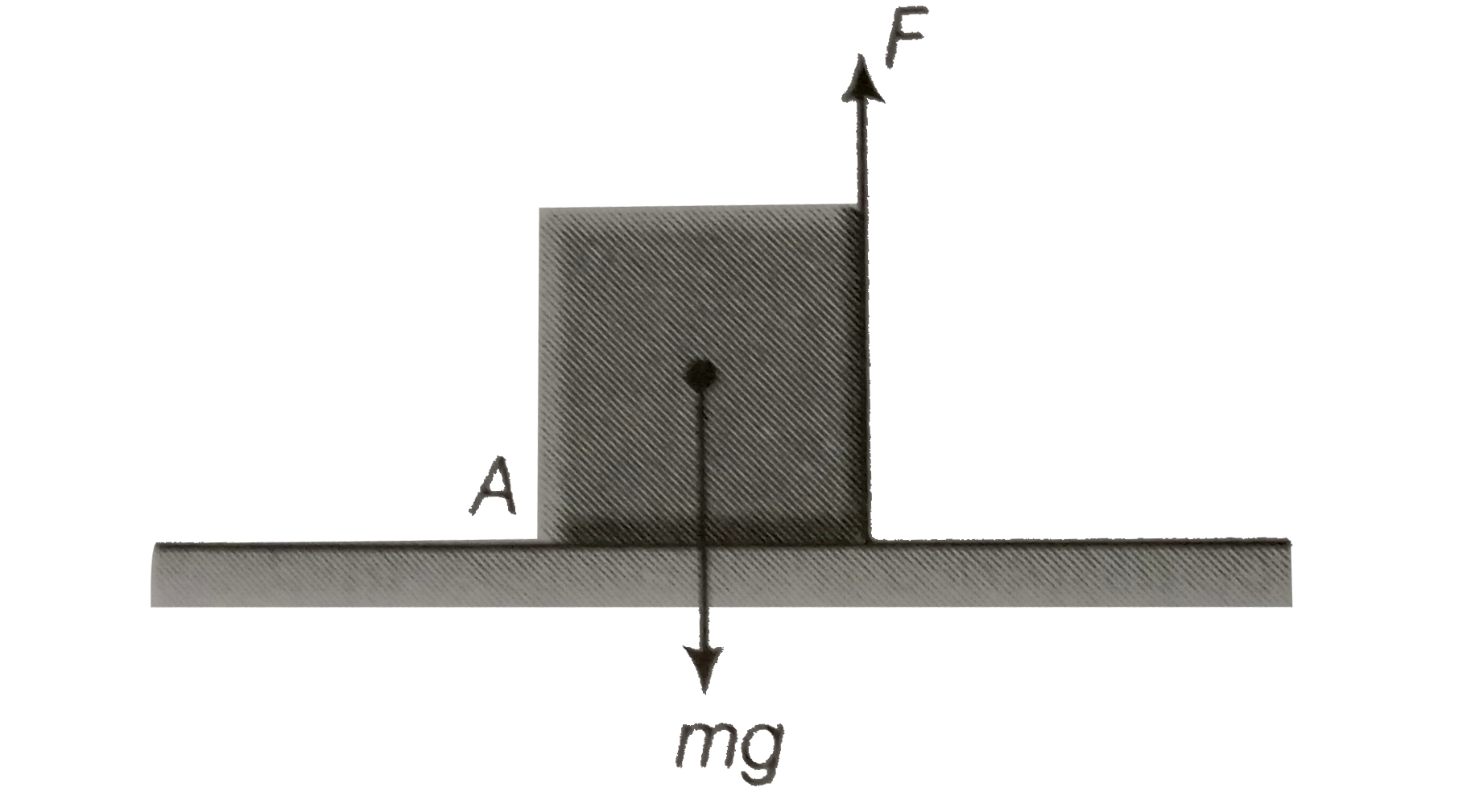
Cube will not exhibit motion ,if $τ_{1} = t a_{2}$
( $∵$ in this case , both the torque will cancel the effect the effect of each other )
$t h e t e f or e f \times a = m g \times \frac{a}{2} \Rightarrow F = \frac{m g}{2}$
Cube will roate only when , $τ_{1} > τ_{2}$
$F \times a > m g \times \frac{a}{2} \Rightarrow F > \frac{m g}{2}$
Let normal reaction is acting at $\frac{a}{3}$ from point A , then
$m g \times \frac{a}{3} = F \times a or F = \frac{m g}{3}$
when $F = \frac{m g}{4}$ which is less than $\frac{m g}{3}$ "" $(F < \frac{m g}{3})$
there will be no motion .
$∴ (a) \to (i i) (b) \to (i i i) (c) \to (i) (d) \to (i v)$

Updated on:21/07/2023