Find the centre of mass of a unifrom (a) half-disc,(b) quarter-disc.
Let M and R be the mass and radius of the half - disc mass per unit area unit aera of the half - disc
m=M12πR2=2MπR2
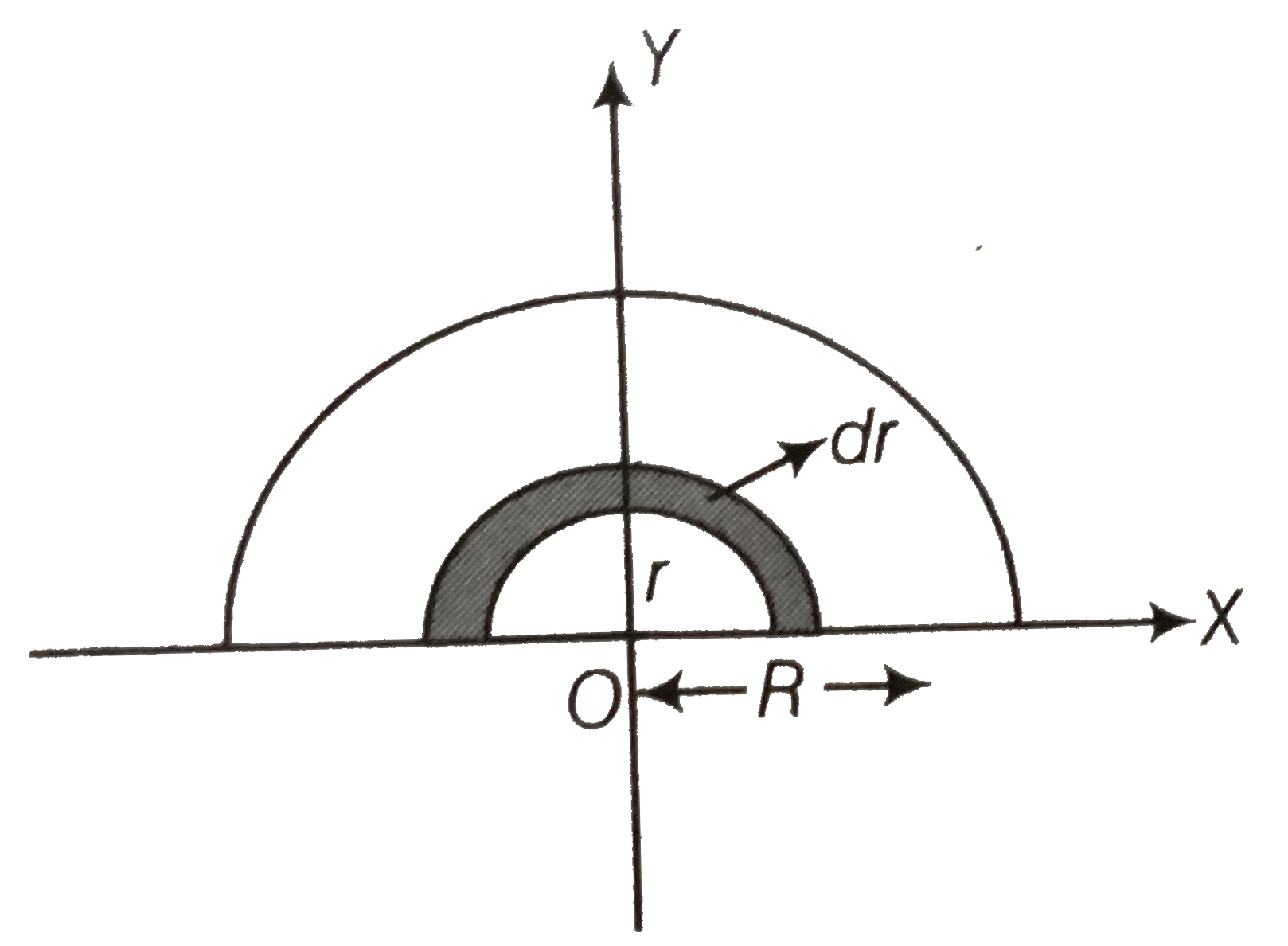
(a) the half -disc can be supposed to be consists of a large number of semicircular rings of mass dm and thickness dr and ranging from r=0 to r=R
Surface area of semicircular ring of radius r and of thickness dr=122πr×dr=πrdr
∴Mass of this elemetary ring dm=πrdr×2MπR2
dm=2MR2rdr
If (x,y) are coordinates of centre of mass of this element,
then, (x,y)=(0,2rπ)
therefore , x=0andy=2rπ
Let xcM and yCM be the coordinates of the centre of the centre of the semicircular disc.
then xCM=1M∫R0xdm=1M∫R0dm=0
yCM=1M∫R0ydm=1M∫R02lπ×(2MR2rdr)
=4πR2∫R0r2dr=4πR2[r33]R0
=4πR2×(R33−0)=4R3π
∴ Centre of mass of the semicicular disc =(9,4R3π)
( b) Centre of mass a unifrom quarter disc,
Mass per unit area of the quarter disc =MπR24=4M3ΠR3
Using symmetry
for a half along y - axis centre of mass will be at x=4R3π
For a half - disc along x-axis centre of mass will be at x=$R3π
Hence , for the quarter disc centre of mass =(4R3π,3R3π)

Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLARCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - very short answer type questions
18 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLARCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - very short answer type questions
18 Videos
- OSCILLATIONSBOOK - NCERT EXEMPLARCHAPTER - OSCILLATIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (MCQs)
40 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLARCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
Similar Questions
Knowledge Check
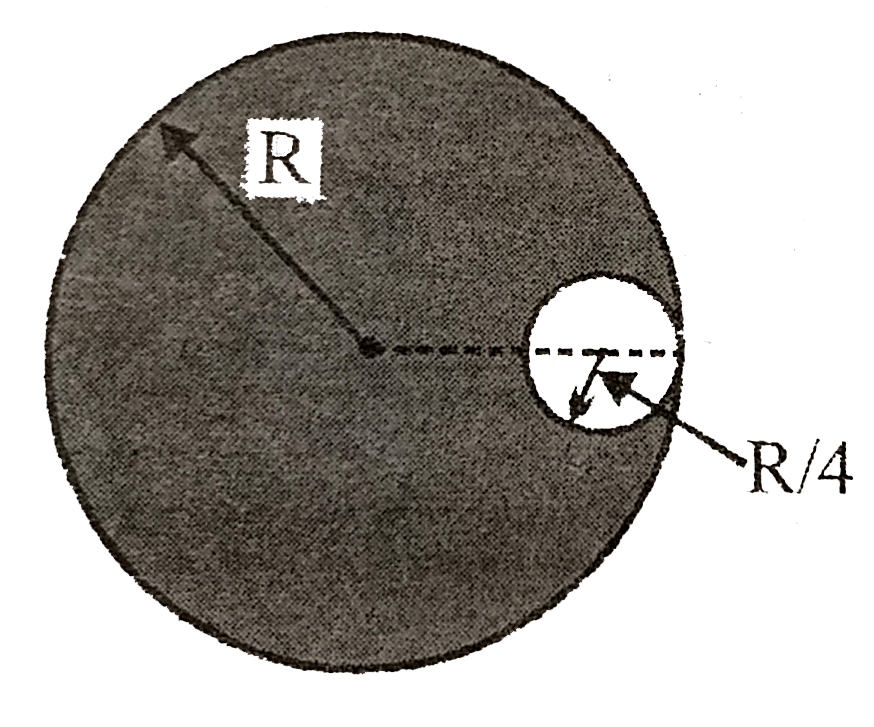
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of OA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
A335cmB135cmC310cmDNone of these
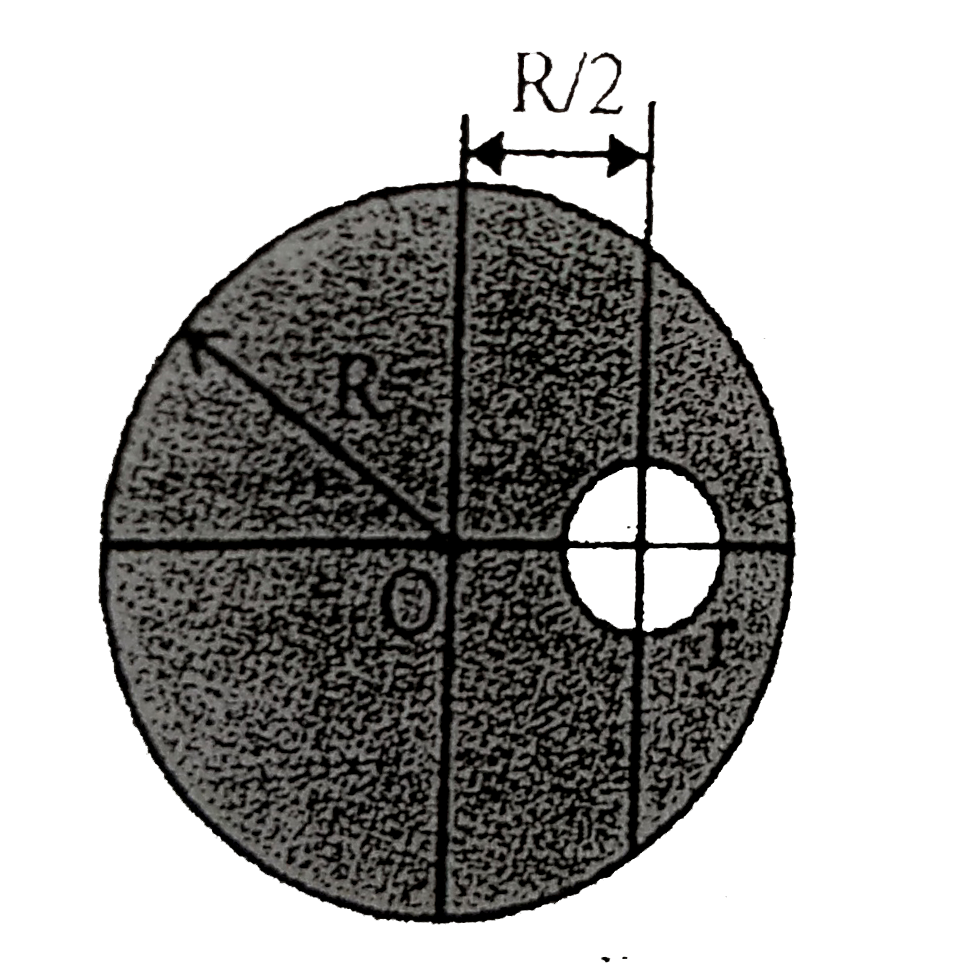
Find the centre of mass of the shaded portion of a disc.
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionFind the centre of mass of the disc shown in figure. . A square is removed from the disc as shown
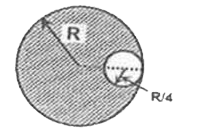
View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.

View SolutionFind the centre of mass xCM of the shaded portion of the disc of radius R=24cm.

View Solution