f(x)=(tanx5)ex3sgnx7 is −
A
An even function
B
An odd fundtion
C
Neither even nor odd function
D
None of these
Video Solution
Text Solution
The correct Answer is:B
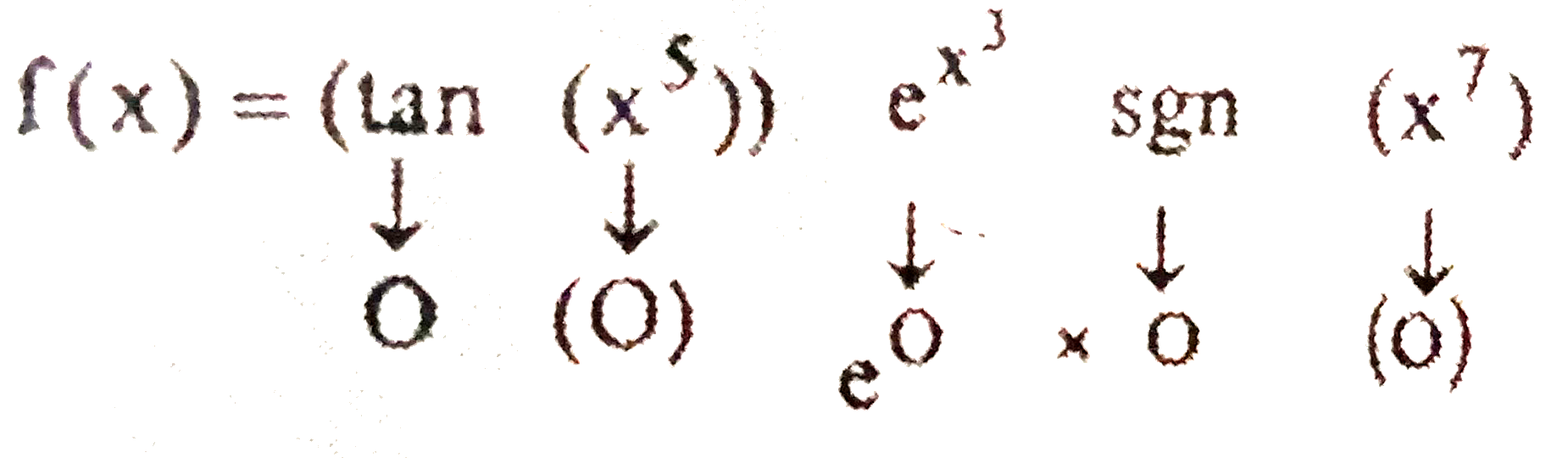
=O×eO×O=O×e∧(E)
=O×E=O.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
f(x)=(sinx7)ex5.Sgn(x9) is:
Aan even functionBan odd functionCneither even nor oddDNone of theseLet f(x)=2tan3x−6tan2x+1+sgn(ex),∀x∈[−π4,π4], Then the positive difference between the least value and the local maximum value of the function is (where sgn (f(x)) represents the signum function)
A7B8C9D10IF f(x)=tanx+e−2x−7x3, then what is the value of f'(0)?
A−2B−1C0D3
If f(x)=x3sgn(x), then
View SolutionFind the range of the following
(i) f(x)=sgn(x2) (ii) f(x)=sgn(x2−2x+3)
View SolutionDomain of the function f(x)=logx2−1x+2+√ex−e2+√sgn(x) is
View SolutionThe range of f(x)=3−|x|−3x+sgn(e−x)+2 (where sgn x denotes signum function of x )
View Solutionf(x)=xsgn(x2) should be
View Solution
