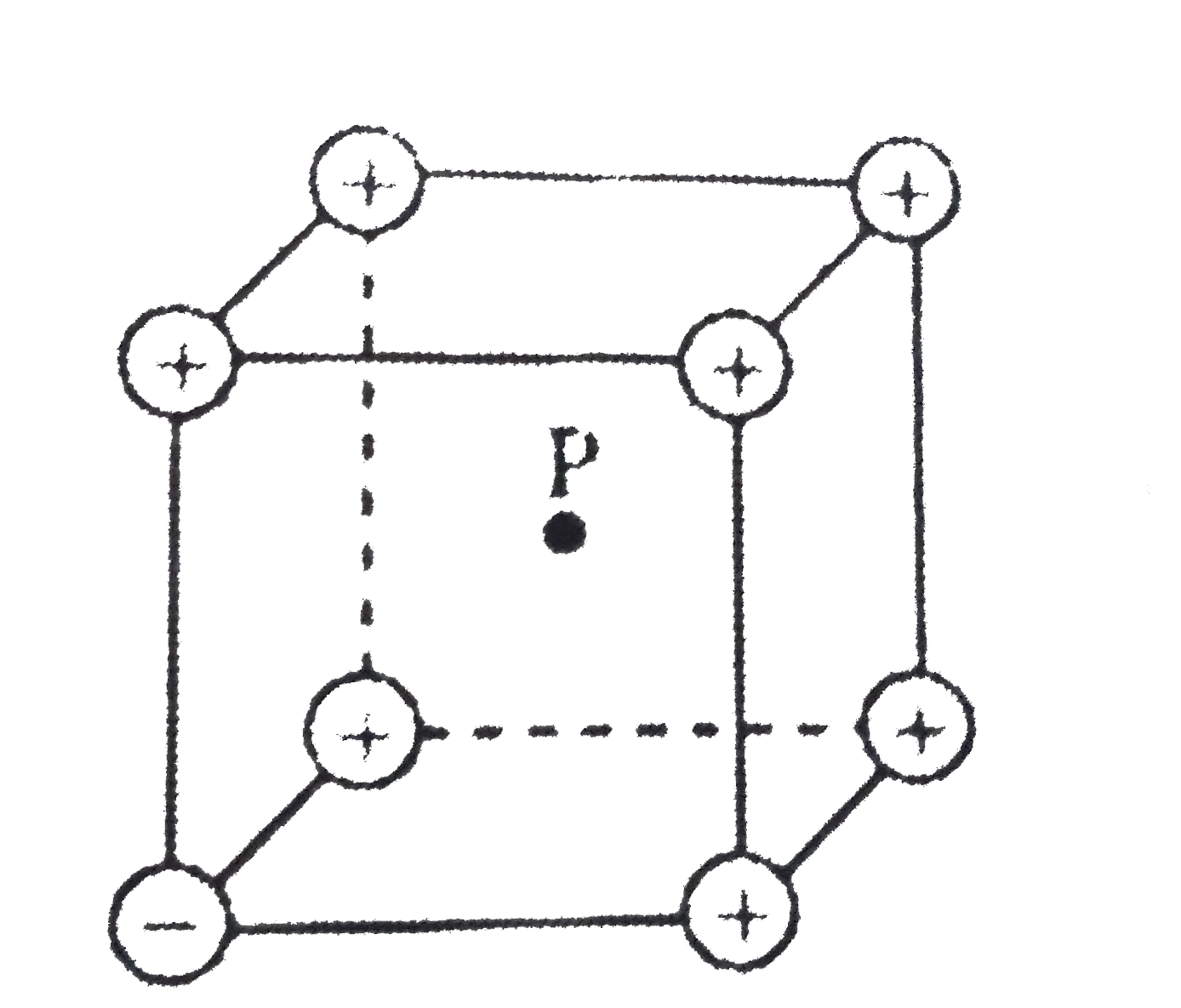
Cosider a regular cube with positive point charge + Q in all corners except for one which has a negative point chnarge -Q .Let the distance from any corner to the centre of the cube be r. what is the magitude of elelctric fleld at point P the centre of the cude ? (K=14πε0)
A
E=7KQ/r2
B
E=KQ/r2
C
E=2KQ/r2
D
E=6KQ/r2
Video Solution
Text Solution
The correct Answer is:C
E=k2Qr2
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A point charge q is kept at e distance x from the centre of a neutral metallic cube.
ANet electric field intensity at the centre is zeroBElectric field intensity due to induced charges on cube at its centre is zero.CElectric field intensity due to point charge at the centre is non-zero.DElectric field intensity at the centre of cube due to point charge and induced charges on cube will be equal in magnitude.A point charge q is kept at a corner of a cube
AElectric flux linked with individual faces of the cube may be zeroBElectric flux linked with individual faces of the cube may be non-zeroCElectric flux linked with a certain face of the cube may be q/8ε0DElectric flux linked with a certain face of the cube may be q/24ε0A charge +q is placed at a distance 'd' from the centre of the uncharged metallic cube of side 'a'. The electric field at the centre of the cube due to induced charges on the cube will be
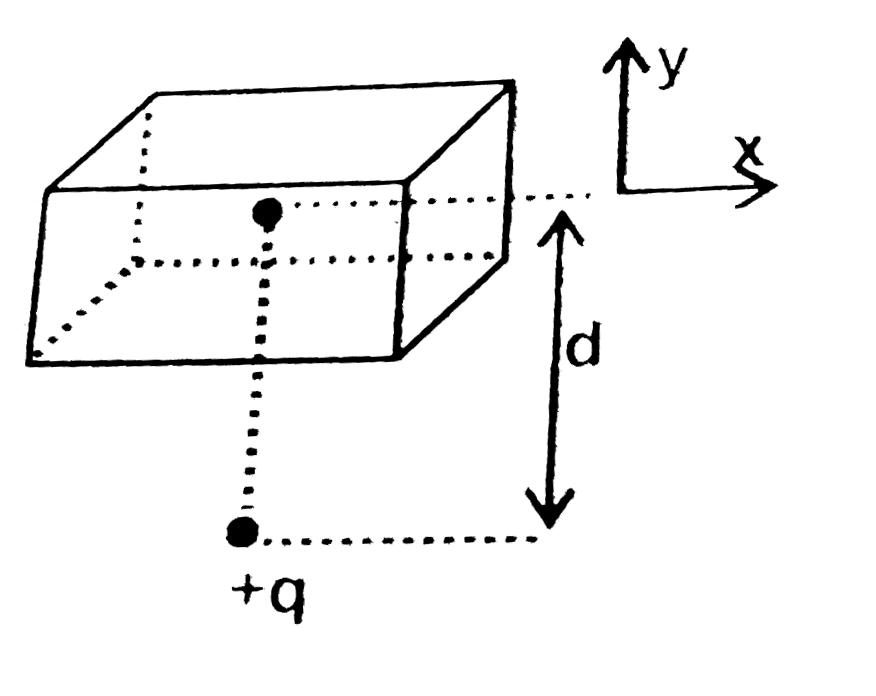 AzeroBq4π∈0d2(−ˆj)Cq4π∈0d2(ˆj)Dq4π∈0(d−a2)(−ˆj)
AzeroBq4π∈0d2(−ˆj)Cq4π∈0d2(ˆj)Dq4π∈0(d−a2)(−ˆj)
If a point charge q is placed at one corner of a cube, what is the flux linked with the cube?
View SolutionIf a point charge q is placed at the centre of a cube.
What is the flux linked (a) with the cube? (b) with each face of the cube?
View SolutionA cube is given and it has -q charge in one corner and +q charges in all the remaining 7 corners. Find the electric field at the center of the cube
View SolutionA point charge q is placed at one corner of a cube of edge a. The flux through each of the cube faces is
View SolutionFour point charges −Q,−q,2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero is
View Solution
