G is the centroid of triangle ABC and $A_{1} and B_{1}$ are the midpoints of sides AB and AC respectively .If $Δ_{1}$ be the area of quandrillateral $Δ / Δ_{1}$ is equal to -

A

3/2

B

3

C

43468

D

none of these

Text Solution

Verified by Experts

The correct Answer is:D

Let P.V . Of A,B & C be

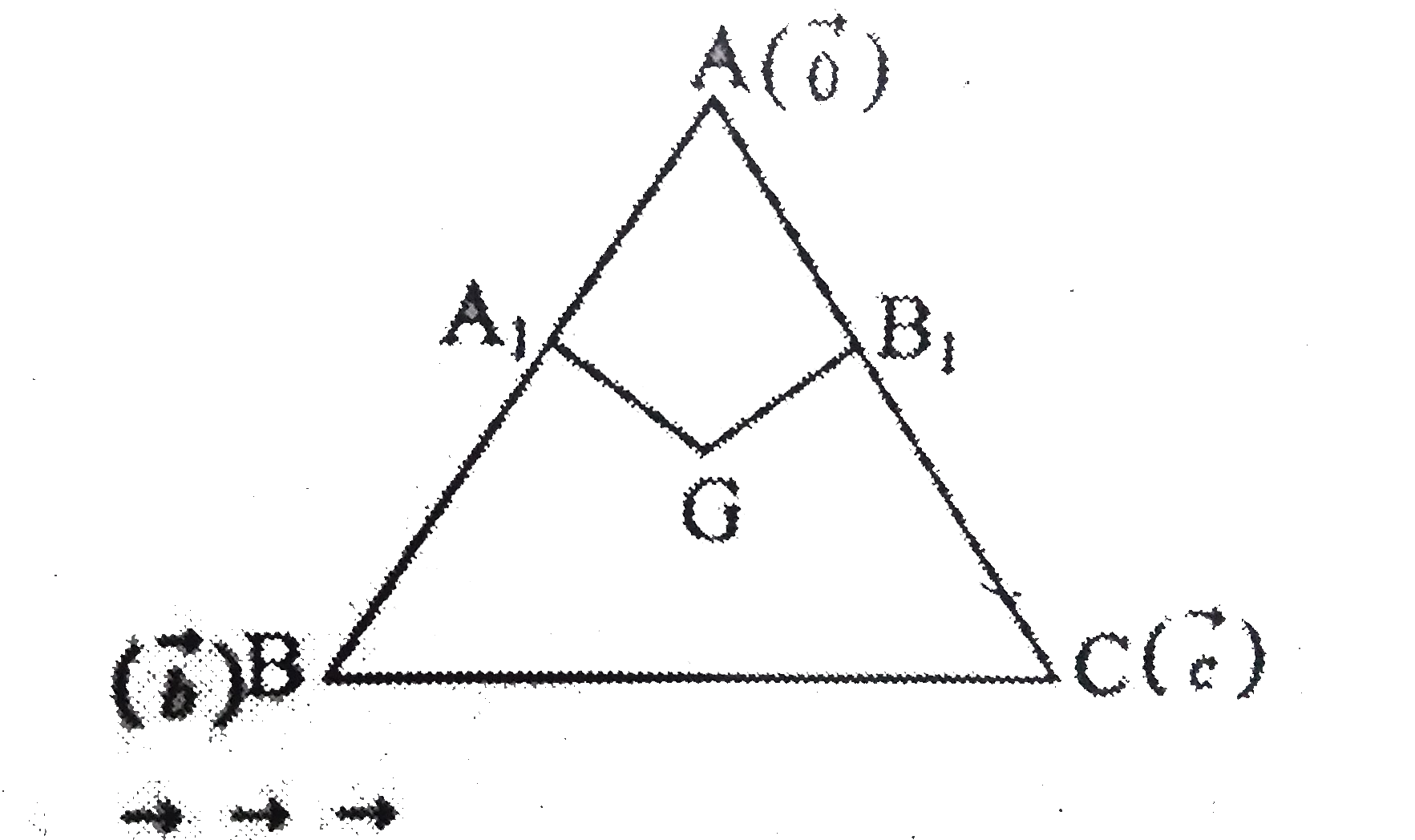
$\to O, \to b, \to c,$ respeccely
$therefore G (\frac{\to b + \to c}{3})$
$A_{1} (\frac{\to b}{2}) & B_{1} (\frac{\to c}{2})$
$Δ_{A B_{1} G} = \frac{1}{2} ∣ ∣ ¯ ¯¯¯¯ ¯ A G \times ¯ ¯¯¯¯¯ ¯ A B_{1} ∣ ∣ = \frac{1}{12} ∣ ∣ \to b \times \to c ∣ ∣$
$Δ_{A A_{1} G} = \frac{1}{2} ∣ ∣ ¯ ¯¯¯¯ ¯ A G \times ¯ ¯¯¯¯¯ ¯ A A_{1} ∣ ∣$
$Δ G A_{1} A B_{1} = \frac{1}{6} ∣ ∣ \to b \times \to c ∣ ∣ = \frac{1}{3} Δ_{A B C} \Rightarrow \frac{Δ}{Δ_{1}} = 3$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

CAREER POINT-MOCK TEST 8-PART (C ) - MATHS

Home
Ask Doubt
Profile