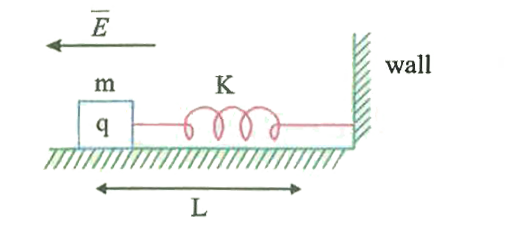
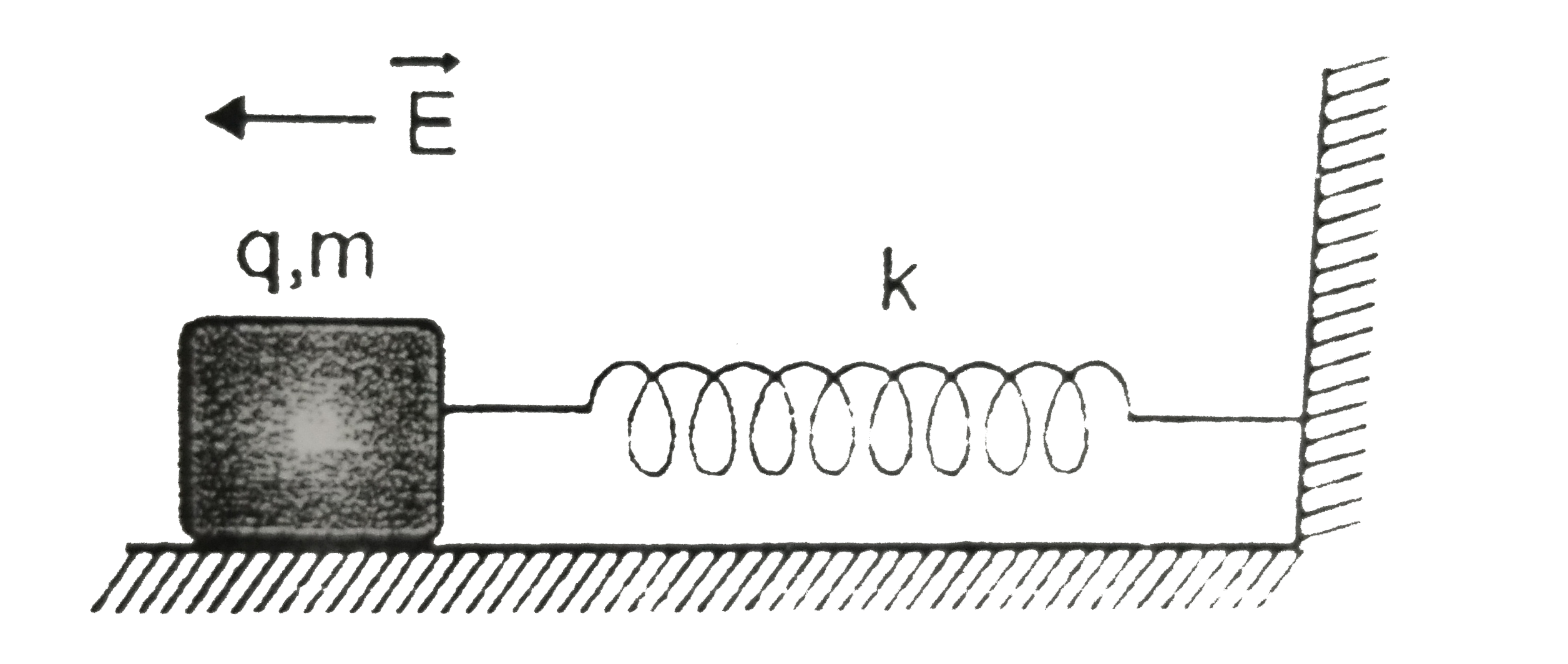
A point mass m and charge q is connected with massless spring of natural length L. Initially spring is in its natural length. If a horizontal uniform electric field E is switched on as shown in figure, then the maximum separation between the point mass and the wall is: (Assume all surface are frictionless)

L+2qEK
L+qEK
L
None of these
The correct Answer is:A
12Kx2=(qE)x
x=2qEK
∴xmax=L+2qEK
Topper's Solved these Questions
Similar Questions
A point mass m and charge q is connected with a spring of negligible mass with natural length L. Initially spring is in natural length. Now a horizontal uniform electric field E is switched on as shwon. Find
a. The maximum separation between the mass and the wall
b.Find the separation of the point mass and wall at the equilibrium position of mass
c. Find the energy stored in the spring at the equilibrium position of the point mass.
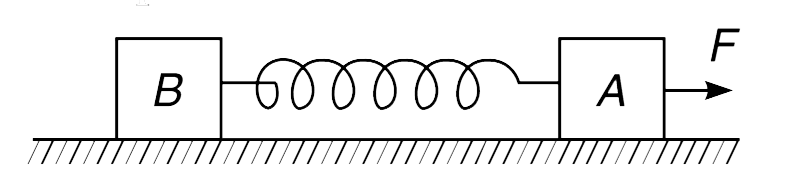
View SolutionTwo blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
View Solution
Knowledge Check
Block A of mass m is placed on a plank B. A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initially spring is in its natural length. If the plank B is given an acceleration a, then maximum compression in the spring is xmak. Find the value of x (All the surface are smooth)
 A12B2C1D4
A12B2C1D4Two blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
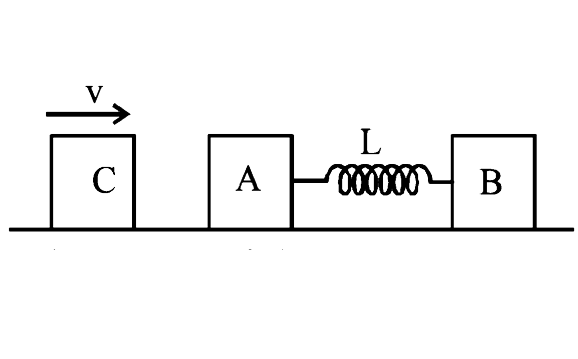 Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)
Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)The system of the wedge and the block connected by a massless spring as shown in the figure is released with the spring in its natural length. Friction is absent. Maximum elongation in the spring will be
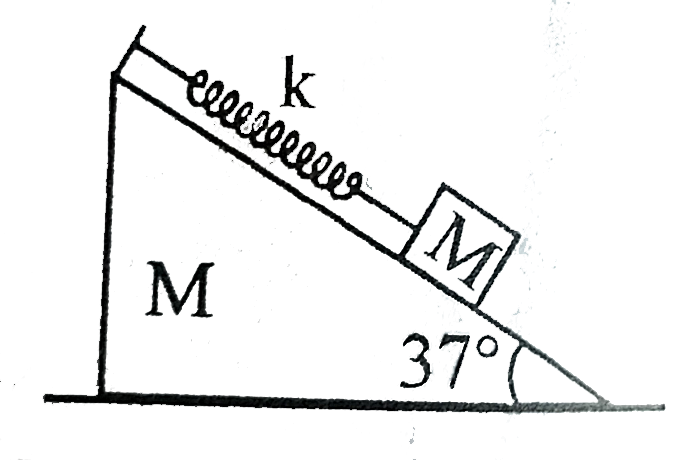 A3Mg5kB6Mg5kC4Mg5kD8Mg5k
A3Mg5kB6Mg5kC4Mg5kD8Mg5k
Method 3 of W
Mass of a piston shown in Fig. is m and area of cross-section is A. Initially spring is in its natural length. Find work done by the gas.

View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionA small cork block of mass m=1kg having charge q=−1C placed on a rough horizontal surface and is connected to a vertical wall through an unstretched non conducting light spring of spring consant k=9N/m as shown in the figure. If a horizontal constant electric field E=10N/C is switched on then the maximum compression in the spring is xm. Find the value of x. (Take g=10m/s2,μ=0.1)
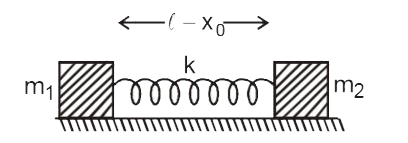
View SolutionTwo blocks of mass m1 and m2 are connected with a spring of natural length l and spring constant k. The system is lying on a smooth horizontal surface. Initially spring is compressed by x0 as shown in figure. Show that the two blocks will perform SHM about their equilibrium position. Also (a) find the time period, (b) find amplitude of each block and (c) length of spring as a function of time.
View SolutionTwo blocks A and H. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View Solution
