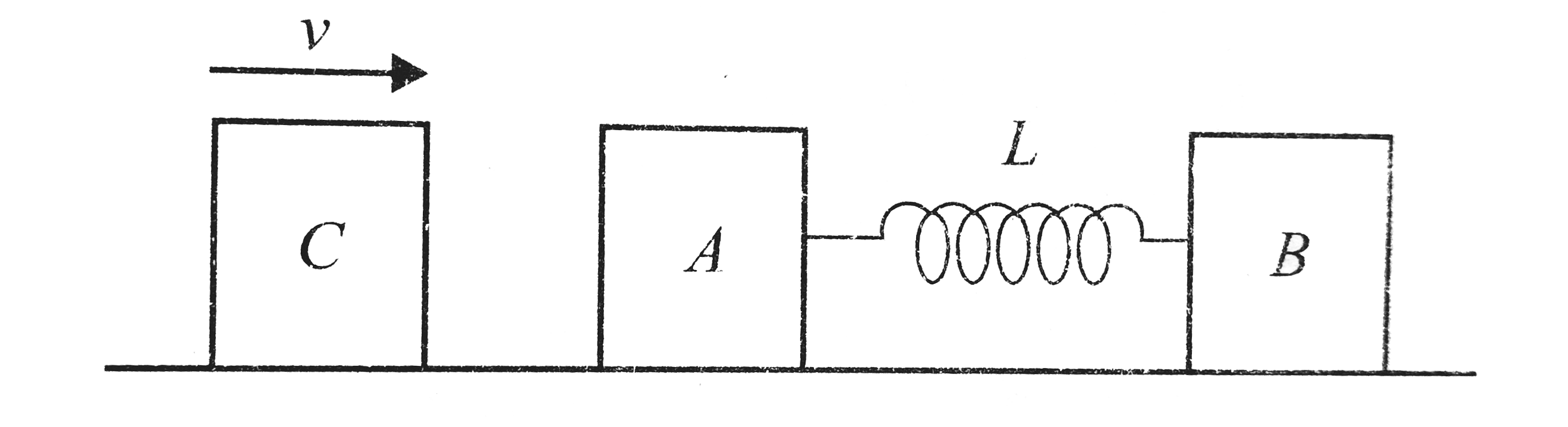
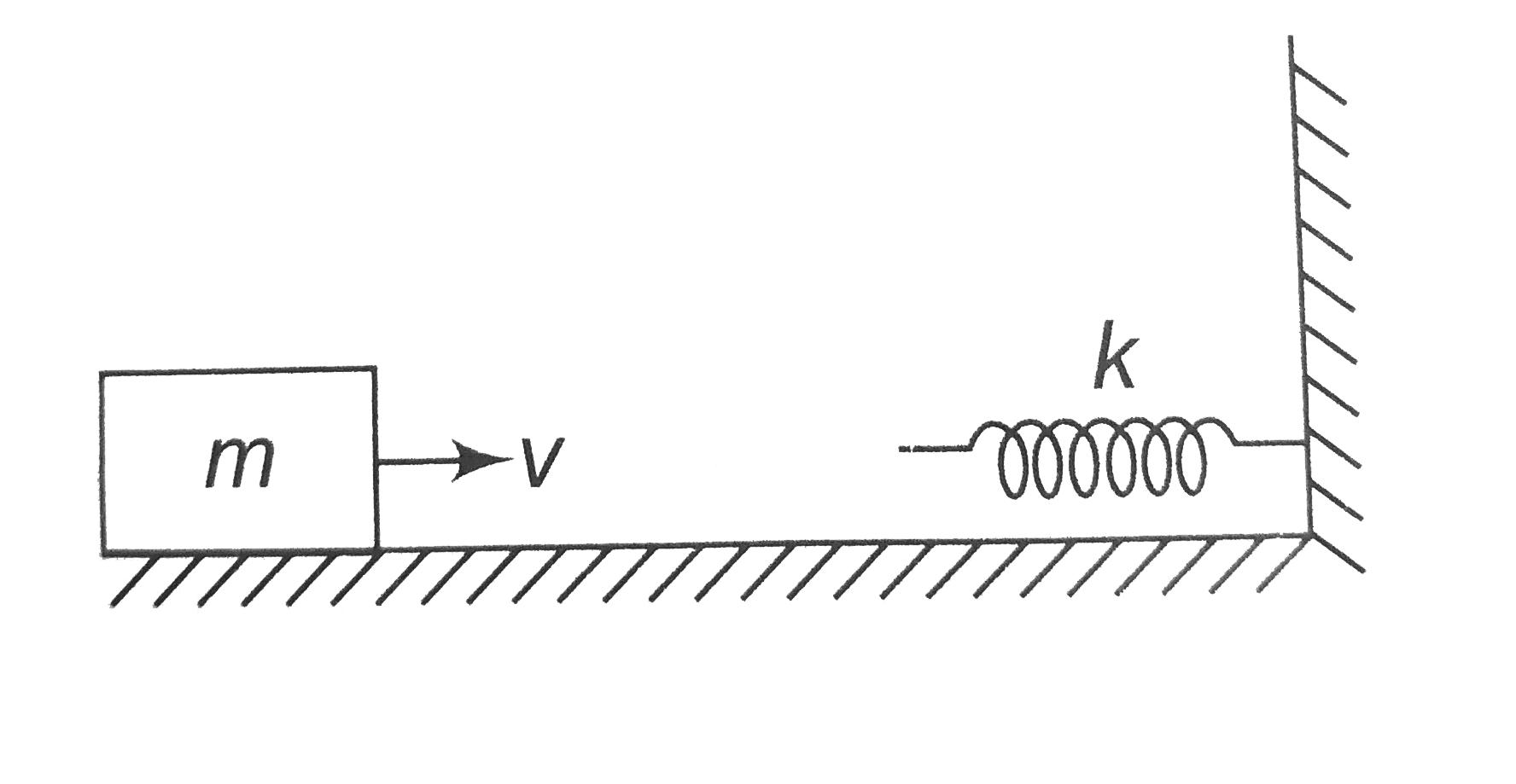
Two blocks A and H. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
the kinetic energy of the A−B system, at maximum compression of the spring, is zero.
the kinetic energy of the A−B system, at maximum compression of the spring, is
the maximum compression of the spring is √(mK)
the maximum compression of the spring is v√(m2K)
The correct Answer is:B, D
In situation i mass C is moving towards right with velocity v,A and B are at rest. In situation ii, which is just after the collision of C with A,C stops and A acquires a velocity v. when A starts moving towards right, the spring suffers a compression due ot which B also starts moving towards right. The compression of the spring continues till there is a relative velocity between A and B. Once this relative velocity becomes zero, both A and B move with the same velocity v' and the spring is in a state of maximum compression.

Applying momentum conservation in situations ii and iii
mv=mv'+mv'⇒v'=v2
Therefore, KE of the system in situation iii is
12mv'2+12mv'2=mv'2=mv24
Applying energy conservation we get
12mv2=12mv'2+12Kx2
solve to get x=v√m2K
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - AR_TYPE1videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - LC_TYPE3videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - SCQ_TYPE12videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Statement I: In an elastic collision between two bodies, the relative speed of the bodies after collision is equal to the relative speed before the collision.
Statement II: In an elastic collision, the linear momentum of the system is conserved.05:15View SolutionA small block of mass M move on a frictionless surface of an inclimed from as down is figure . The engle of the inclime suddenly change from 60∘ to 30∘ at point B . The block is initally at rest at A Assume the collsion between the block and the incline are totally inclassic (g=10m/s2)
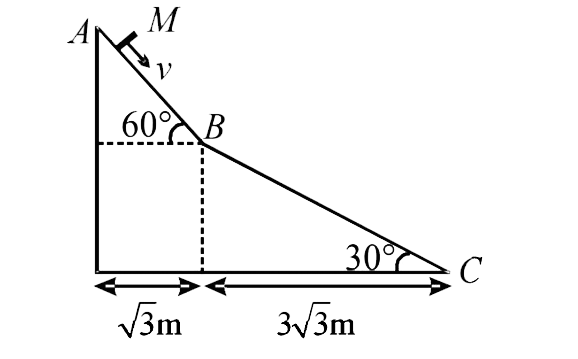
The speed of the block at point B immedutaly after it strikes the second inclime is - 03:37View Solution
03:37View SolutionTwo paricle A and B initially at rest, move towards each other under mutual force of attraction. At the instant when the speed of A is V and the speed of B is 2V, the speed of the centre of mass of the system is
08:22View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.504:08View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
05:13View SolutionTwo blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
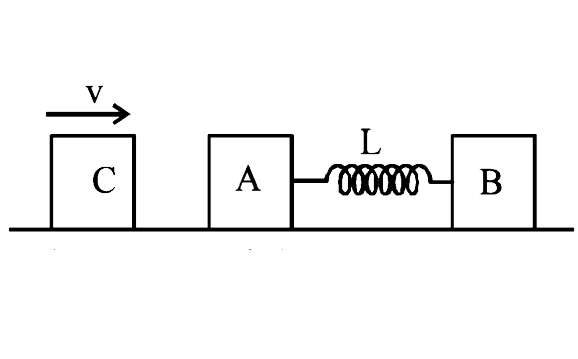 06:38View Solution
06:38View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 03:43View Solution
03:43View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.
 View Solution
View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k , with the spring at its natural length. A third identical block C (mass m ) moving with a speed v along the line joining A and B collides with A . The maximum compression in the spring is
View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)04:08View SolutionTwo blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -
07:21View SolutionTwo identical blocks A and B, each of mass m resting on smooth floor, are connected by a light spring of natural length L and the spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is proportional to
03:08View SolutionTwo blocks of masses m, and m, are connected to the ends of a spring of spring constant k. System is kept at rest on a frictionless horizontal floor with spring in its natural length. Both the blocks are pulled along opposite directions with forces of same magnitude F. Calculate maximum elongation of spring and distances travelled by the blocks during this motion.
05:15View SolutionTwo blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in figure below. A third identical bloack C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides with A. Then :
 03:08View Solution
03:08View SolutionTwo identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
03:29View Solution

