In an equilateral triangle ABC, AL, BM, and CN are medians. Forces along BC and BA represented by them will have a resultant represented by
2AL
2BM
2CN
AC
The correct Answer is:2
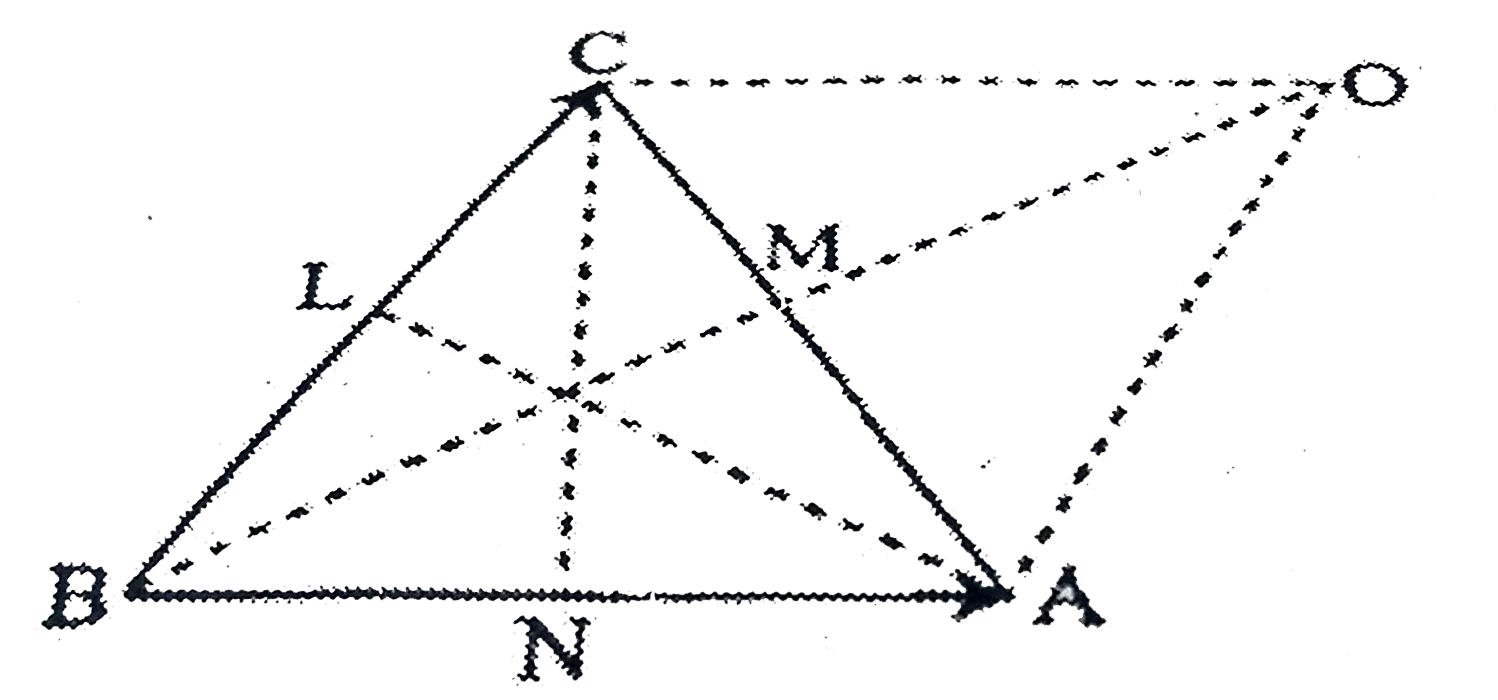
∵¯¯¯¯¯¯BO=¯¯¯¯¯¯BA+¯¯¯¯¯¯BC
=2¯¯¯¯¯¯¯BM
Topper's Solved these Questions
Similar Questions
An equilateral triangle ABC has its centroid at the origin and the base BC lies along the line x+y=1. Area of the equilateral ΔABC is
View SolutionΔABC is an equilateral triangle and D and E are midpoints of AB and BC respectively. Then the area of ΔABC : the area of the trapezium ADEC is
View Solution
Knowledge Check
In an equilateral ΔABCif AD⊥BC, then
A2AB2=3AD2B3AB2=4AD2C5AB2=6AD2D4AB2=5AD2In an equilateral triangle ABC, the side BC is trisected at D. Then the correct relation is
A9AD2=7AB2B8AD2=9AB2C7AD2=9AB2Dnone of theseIn an equilateral triangle ABC, the side BC is trisected at D. Then the correct relation is
A9AD2=7AB2B8AD2=9AB2C7AD2=9AB2DNone of these
If ABC is an equilateral triangle and D is a point on BC such that AD⊥BC, then
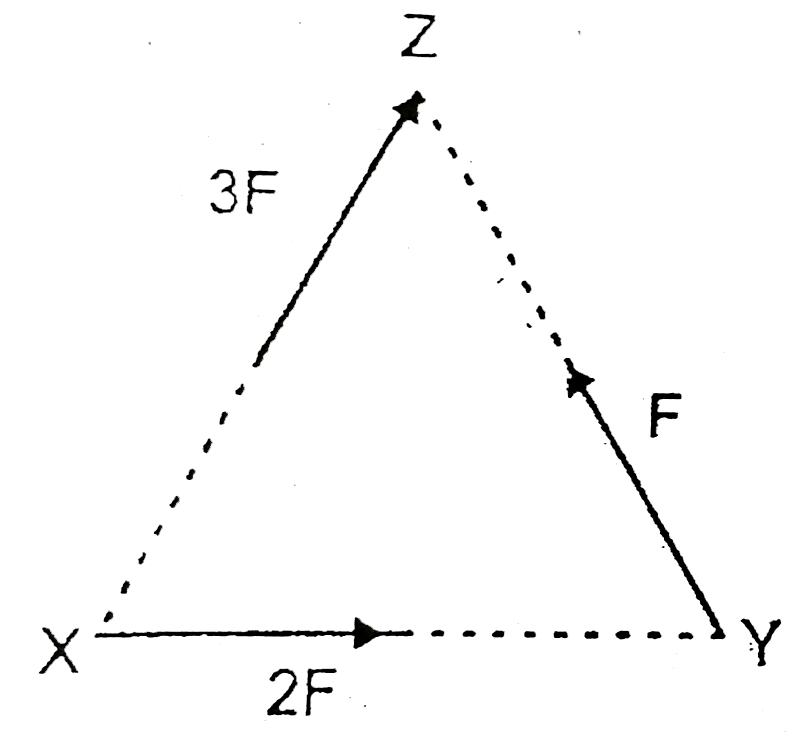
View SolutionIf XYZ is an equilateral triangle. Then the resultant of the three forces shown in the figure is :
View SolutionConsider the two equiangular triangles ABC and DEF having medians as ALandDMrespectively as shown in figure below.
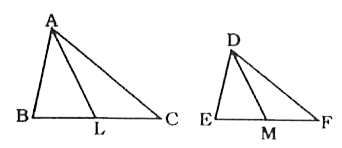
View SolutionConsider the two equiangular triangles ABC and DEF having medians as ALandDMrespectively as shown in figure below.

View SolutionConsider the two equiangular triangles ABC and DEF having medians as ALandDMrespectively as shown in figure below.

View Solution
