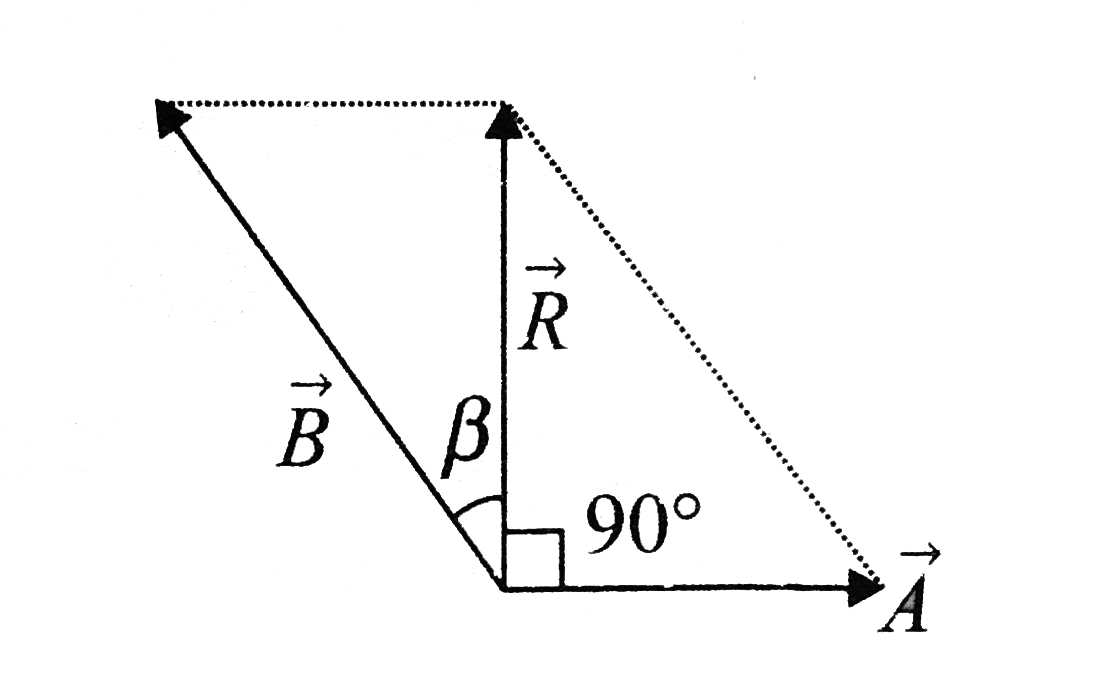
The resultant of two vectors $\to P$ and $\to Q$ is $\to R$ . If the magnitude of $\to Q$ is doubled, the new resultant vector becomes perpendicular to $\to P$ . Then, the magnitude of $\to R$ is equal to

A

P + Q

B

P

C

P - Q

D

Q

Video Solution

Text Solution

Verified by Experts

The correct Answer is:4

${tan 90}^{\circ} = \frac{2 Q sin θ}{p + 2 Q cos θ}$

$\Rightarrow P + 2 Q cos θ = 0$
$& R^{2} = P^{2} + Q^{2} + 2 P Q cos θ$
$= Q^{2} + P (P + 2 Q cos θ)$
$= Q^{2} + 0$
$\Rightarrow R = Q$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The resultant of two vectors $\to P$ and $\to Q$ is $\to R$ . If $\to Q$ is doubled then the new resultant vector is perpendicular to $\to P$ . Then magnitude of $\to R$ is :-
A $\frac{P^{2} - Q^{2}}{2 P Q}$
B $Q$
C $\frac{P}{Q}$
D $\frac{P + Q}{P - Q}$
Question 2 - Select One
The resultant $\to P and \to Q$ is perpendicular to $\to P$ . What is the angle between $\to P and \to Q$ ?
A ${cos}^{- 1} (P / Q)$
B ${cos}^{- 1} (- P / Q)$
C ${sin}^{- 1} (P / Q)$
D ${sin}^{- 1} (- P / Q)$
Question 3 - Select One or More
if $\to P \times \to R = \to Q \times \to R$ , then
A $\to P = \to Q$
B $\to P$ and $\to Q$ need not be equal
CThere are infinite number of possibilities for $\to P$ (If $\to Q$ and $\to R$ are given ) which satisfy this relationship.
D $\to p$ and $\to Q$ must be coplanar

CAREER POINT-UNIT TEST 1-PHYSICS

Home
Ask Doubt
Profile