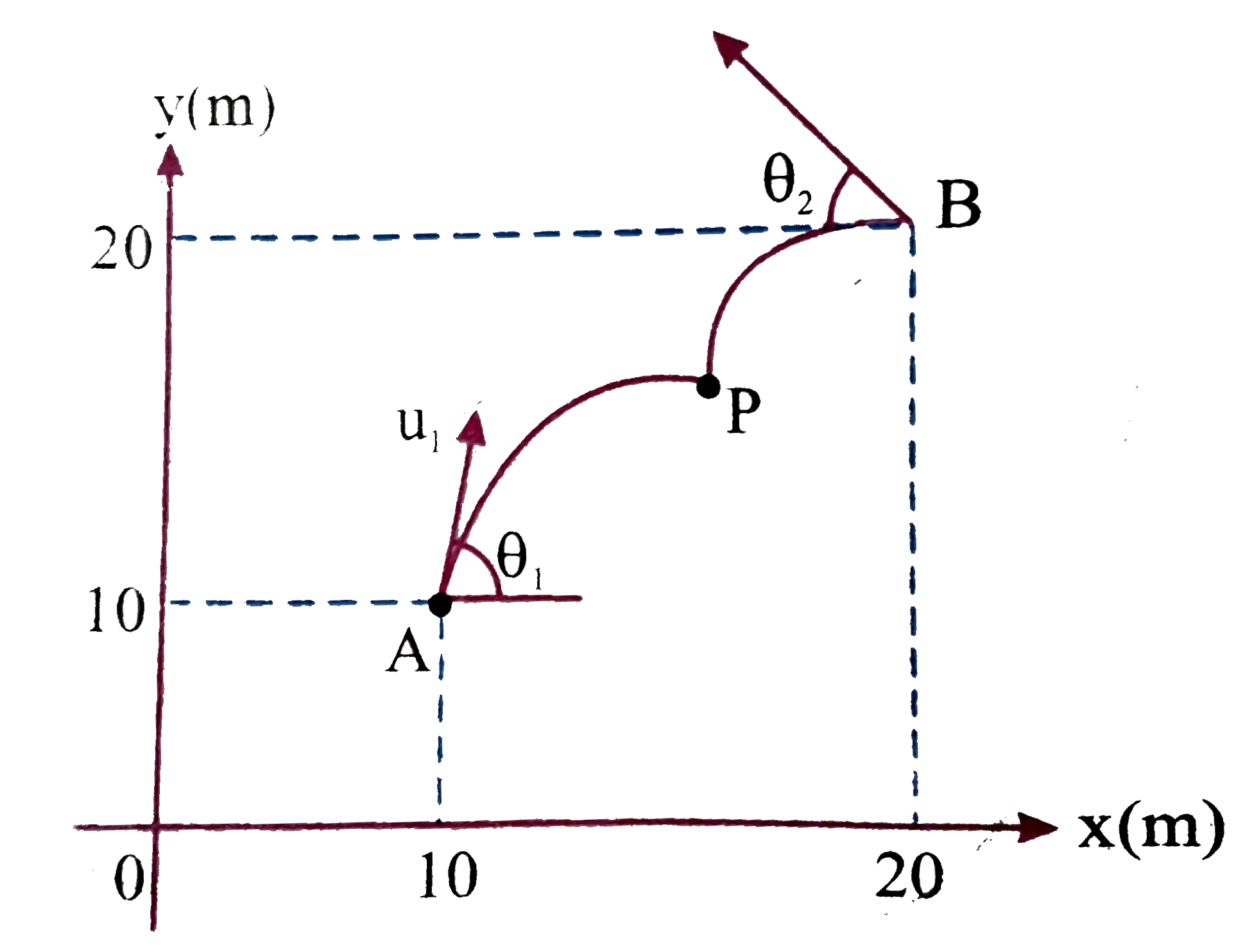
Two particles are projected simultaneously from the level ground as shown figure. They may collide after a time :
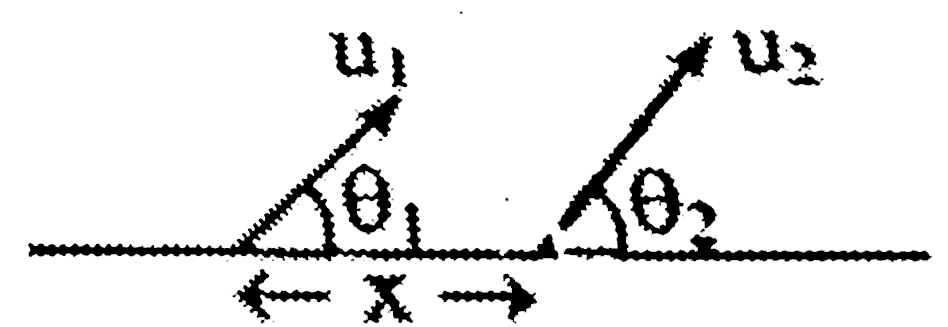
xsinθ2u1
xcosθ2u2
xsinθ2u1sin(θ2−θ1)
xsinθ1u2sin(θ2−θ1)
The correct Answer is:3
t=xu1cosθ1−u2cosθ2 ...(i)
And u1sinθ1.t−12gt2=u2sinθ2.t−12gt2
∴u1sinθ1=U2sinθ2 ...(ii)
from equation no.(i)&(ii)
t=xu1cosθ1−u1sinθ1.cosθ2sinθ2
∴t=xsinθ2u1sin(θ2−θ1)
Topper's Solved these Questions
Similar Questions
Two particles A and B are projected simultaneously in a vertical plane as shown in figure. They collide at time t in air. Write down two necessary equations for collision to take place.

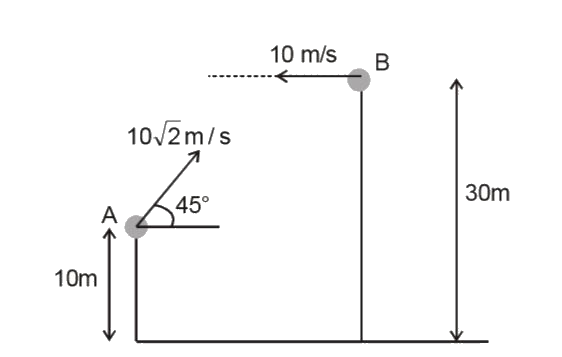
View SolutionTwo projectiles are projected simultaneously from two towers as shwon in figure. If the projectiles collide in the air, then find the distance "s" between the towers.
View Solution
Knowledge Check
Two particles are projected simultaneously from the top of the towers as shown. Find the distance between the towers if they collide in mid air during their flight.
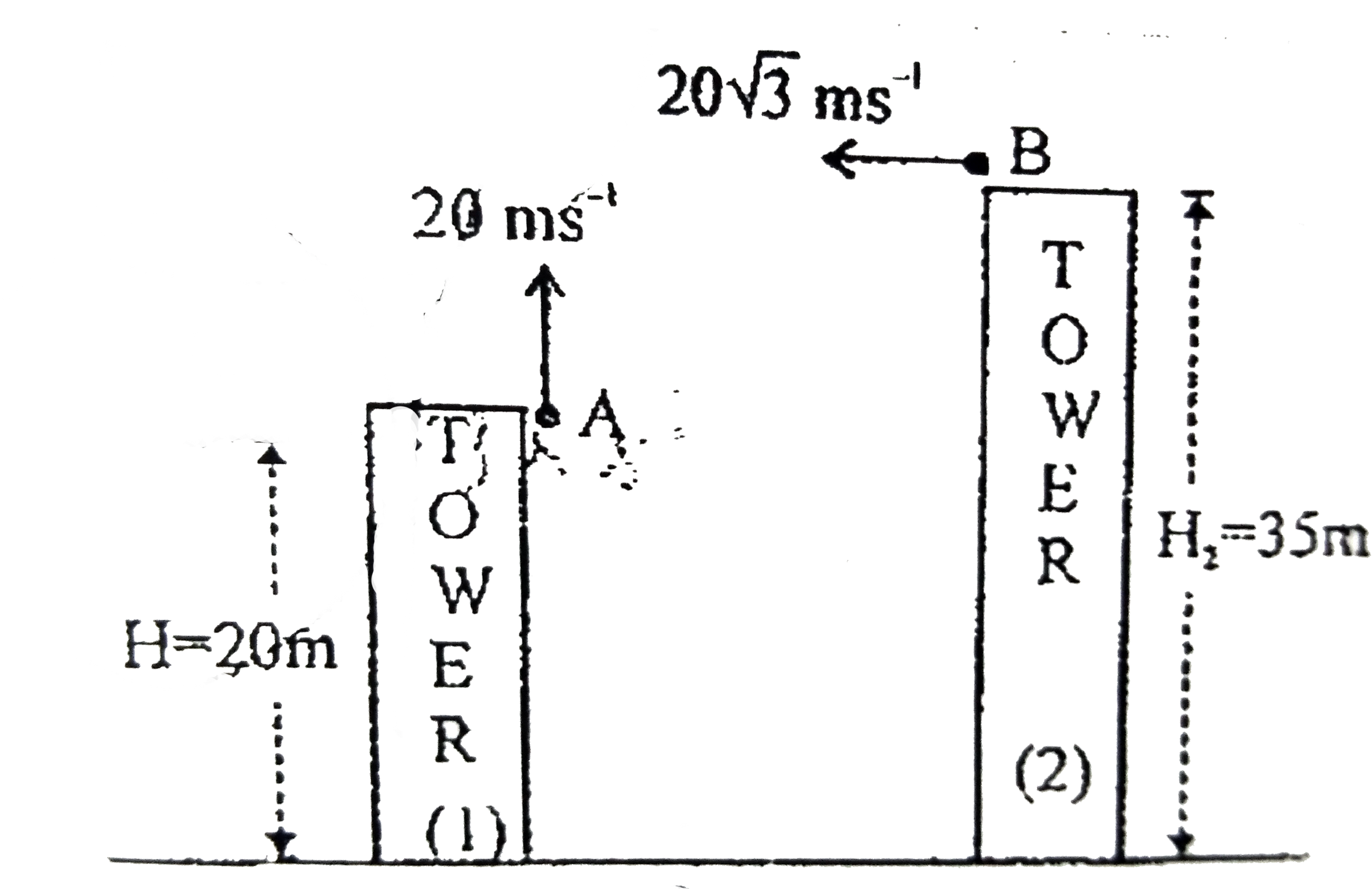 A15mB20mC15√3mD5√3m
A15mB20mC15√3mD5√3mTwo particles P & Q are projected simultaneously from a point O on a level ground in the same vertical plane with the same speed in directions making angle of 30∘ and 60∘ respectively with the horizontal.
ABoth reach the ground simultaneouslyBP reaches the ground earlier than QCBoth strike the same point on the level groundDThe maximum height attained by Q is thrice that attained by PTwo particles P and Q are projected simultaneously away from each other from a point A as shown in figure. The velocity of P relative to Q in ms−1 at the instant when the motion of P is horizontal is
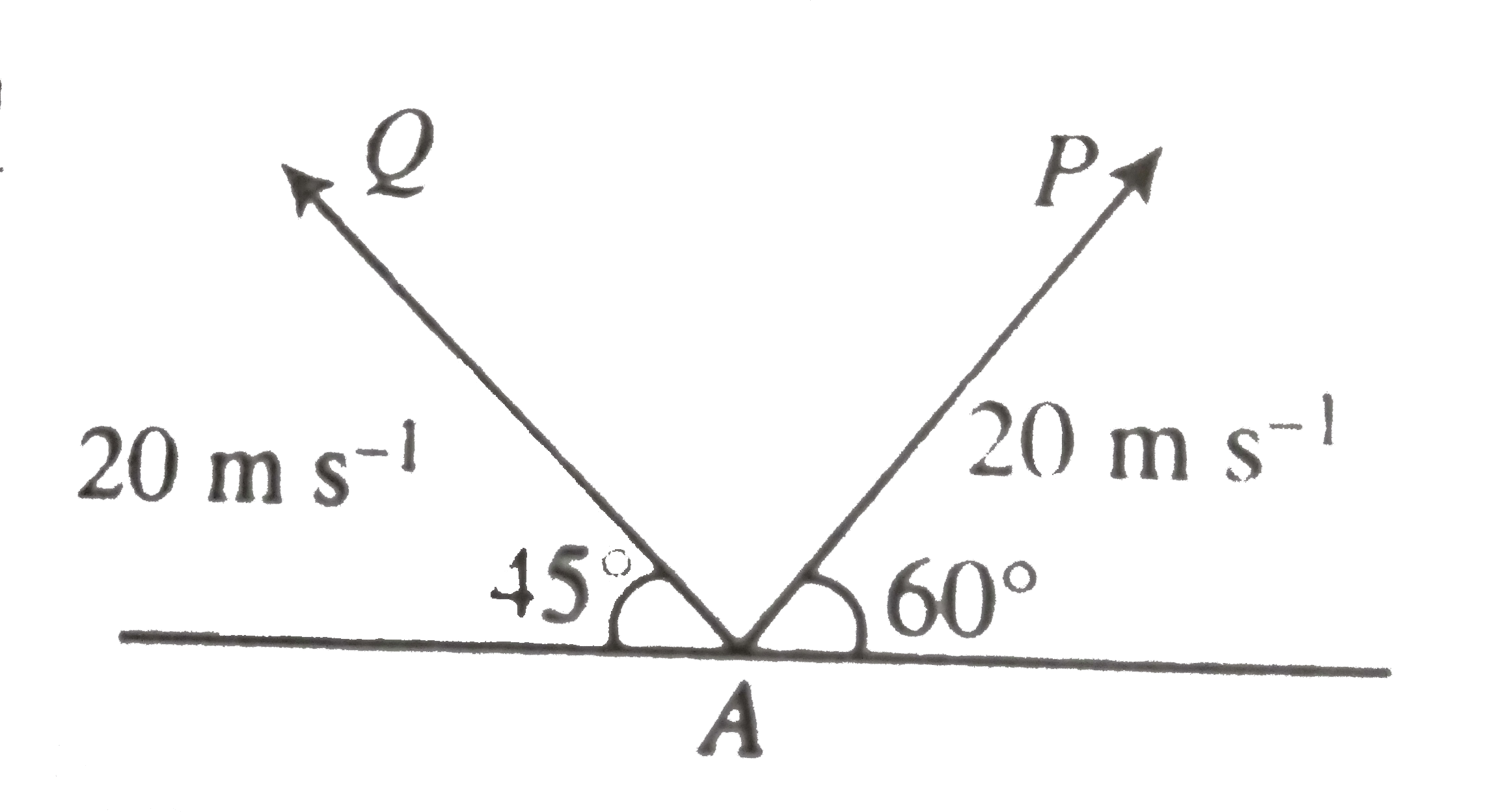 A10√4−√3B20√4−√3C10√4+√3D20√4+√3
A10√4−√3B20√4−√3C10√4+√3D20√4+√3
Two particles A and B are projected simultaneously in the directins shown in figure with velocities vA=20m/sandvB=10m/s respectively. They collide in air after 12 s. Find
(a) the angle θ
(b) the distance x.
 .
.
View SolutionTwo particles are projected from the two towers simultaneously, as shown in the figure. What should be value of 'd' for their collision.

View SolutionTwo projectiles A and B are fired simultaneously as shown in figure. They collide in air at point at time t.Then
View SolutionTwo particles are projected simultaneously from two different points in a uniform gravitational field and collide with each other at a point Q(2b,3b). In the absence of the field they would have collided at P(2b,8b) in a time t0. The acceleration due to gravity at this place g must be equal to
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:

View Solution
