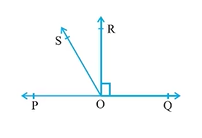
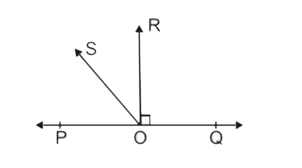
In Fig. 6.17, POQ is a line. Ray OR is
perpendicular to line PQ. OS is another ray lying between rays OP and OR.
Prove that ∠ROS=12(∠QOS−∠POS).
Step by step video solution for In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that /_R O S=1/2(/_Q O S-/_P O S)dot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, POQ is a line. Ray OR is perpendicular to lien PQ.OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS)
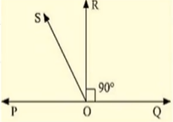
View SolutionIn figure POQ is a line. Raw Oris perpendicular to line PQ .OS is another ray lying between rays OP and OR. Prove that ∠ROS12(∠QOS−∠POS)i.e.,∠1=12(∠2−∠3)
View Solution
Knowledge Check
In arrangement shown in figure, plane wavefront of monochromatic light of wavelength λ is incident on identical slits S1 and S2. There is another pair of indentical slits S3 and S4 which are having separation Z=λD2d Point O is on the screen at the common perpendicular bisector of S1S2 and S3S4.I1 is the intensity at point O Now the board having slits S3S4 is moved upward parallel to itself and perpendicular to line AO till slit S4 is on line AO and it is observed that now intensity at point O is I2 then I2I1 is :
 A12B2C1D0
A12B2C1D0
In Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

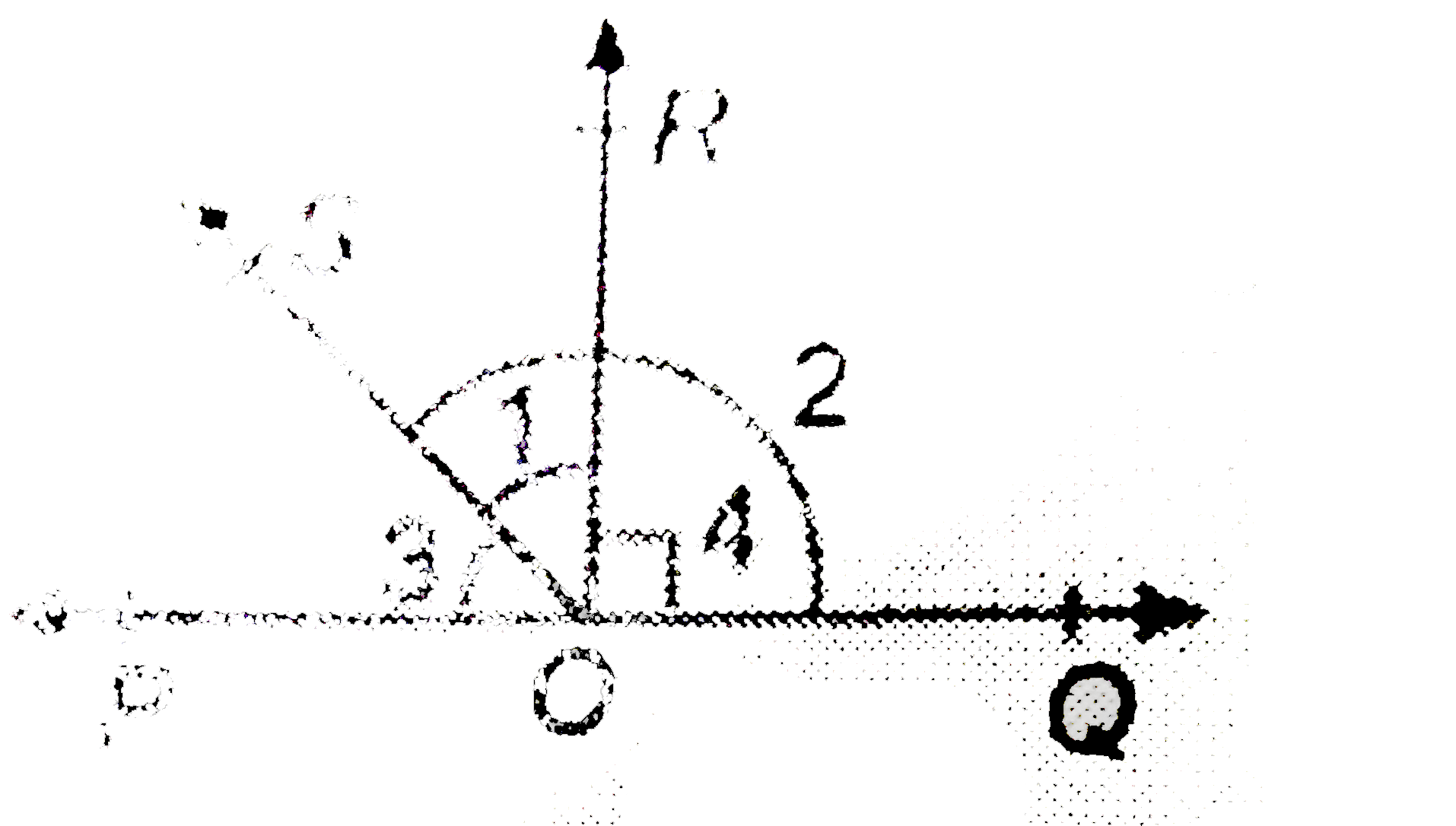
View SolutionPOQ is a straight line RO⊥PQ , SO is a ray from O then prove that ∠ROS=12(∠QOS−∠POS)
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.

View SolutionIf P + Q = R and P - Q = S, prove that R2+S2=2(P2+Q2)
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.

View SolutionIn Fig, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR=130∘ and S is a point on the circle, find ∠1+∠2.
View Solution
