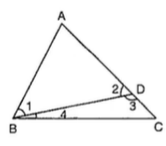
The sum of any two sides of a triangle is greater than the third side. GIVE : A ABC
Video Solution
Text Solution
In△ABC,
extend AB to D in such a way that AD=AC.
In△DBC
as the angles opposite to equal sides are always equal, so,
∠ADC=∠ACD
Therefore,
∠BCD>∠BDC
As the sides opposite to the greater angle is longer, so,
BD>BC
AB+AD>BC
Since AD=AC then,
AB+AC>BC
similarly,
AB+BC>AC
BC+AC>AB
Hence, sum of two sides of a triangle is always greater than the third side.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The sum of length of two sides of a triangle is always
Aless than thirdBgreater than thirdCequal to thirdD23 to third
Sum of any two sides of a triangle is not less than the third side
View SolutionThe sum of any two sides of a triangle is _______ than the third side .
View SolutionThe sum of any two sides of a triangle is always ...... than the third side.
View SolutionTheorem 7.8 : The sum of any two sides of a triangle is greater than the third side.
View SolutionSum of any two angles of a triangle is always greater than the third angle.
View SolutionShow that the difference of any two sides of a triangle is less than the third side. GIVEN : ABC TO PROVE : (i) AC−AB<BC BC−AC<AB (iii) BC−AB<AC CONSTRUCTION : Take a point D on AC such that AD=AB. Join BD.
 View Solution
View SolutionThe difference of any two sides of a triangle is _______ than the third side .
View Solution

