If D is the mid-point of the hypotenuse AC of a right triangle ABC , prove that BD=12AC . GIVEN : A ABC in which ∠B=900 and D is the mid-point of AC. TO PROVE : BD=12AC CONSTRUCTION Produce BD to E so that BD=DE. Join EC.
In∠ADBand∠CDE
AD=CD(O is midpoint of AC)
BD=DE(given)
∠ADB=∠CDE(UDA)
∠ADB≅∠CDE(SAS)
EC=ABand∠CED=∠ABP
In∠ABCand∠ECB
AB=EC(proved above)
BC=BC(common)
∠ABF=∠ECB(90)
∠ABC≅∠ECB(SAS)
AC=BE
12AC=12BE
12AC=BD.
Topper's Solved these Questions
Similar Questions
Prove that any two sides of a triangle are together greater than twice the median drawn to the third side. GIVEN : ABC in which AD is a median. PROVE : AB+AC>2AD CONSTRUCTION : Produce AD to E such that AD=DE. Join EC.
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionA point D is taken on the side BC of a ABC such that BD=2DC. Prove that ar ( ABD)= 2 ar ( ADC)
View SolutionABCD is a parallelogram X and Y are the mid-points of BC and CD respectively. Prove that ar(AXY)=38ar(∣∣gmABCD)
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionIf D,E,F are the mid-points of the sides BC,CAandAB respectively of a triangle ABC, prove by vector method that AreaofDEF=14(areaofABC).
View SolutionThe sum of any two sides of a triangle is greater than the third side. GIVE : A ABC
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
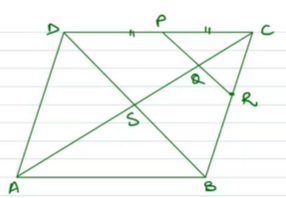View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
View Solution