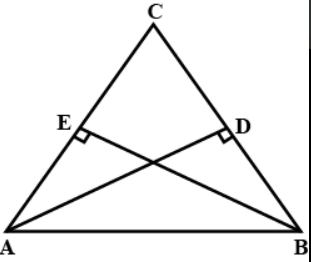
AD and BE are respectively altitudes of triangle ABC such that AE=BD. Prove that AD=BE.
Video Solution
Text Solution
AD=BE
∠AEBand∠BDA
AB=BA(hypotenuse)
AE=BD(given)
∠AEB≅∠BDA(HL)
EB=DA
BE=AD.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, BD and CE are the altitudes of triangle ABC such that BD = CE, then

∠DCB=A∠EBCB∠ECBC∠ABDD∠DBC - Question 2 - Select One
If AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
A△ABHB△BDHC△ABDD△BEA
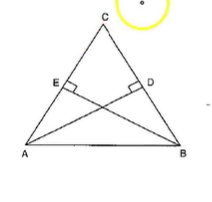
In Figure, AD and BE are respectively altitudes of ABC such that AE=BD. Prove that AD=BE.
 View Solution
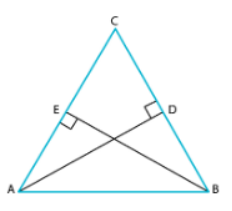
View SolutionIn Figure, aAD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC. Prove that AE=BD
 View Solution
View SolutionIn Figure, if AB=AC and BE=CD, prove that AD=AE.
 View Solution
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
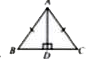
AD bisects BCView SolutionIn Figure, AD=AE and D and E are points on BC such that BD=EC. Prove that AB=AC
 View Solution
View SolutionD is a point on the circumcircle of ΔABC in which AB=AC such that B and D are on the opposite sides of AC. If CD is produced to a point E such that CE=BD. Prove that AD=AE.
View Solution