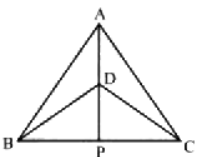
ABC
and
DBC
are
two isosceles triangles on the same base BC
and
vertices A
and
D
are
on the same side of BC
.
If AD
is
extended to intersect BC
at
P,
show
that
ABD≅ACD
(ii) ABP≅ACP
AP
bisects ∠A
as well as ∠D
AP
is
perpendicular bisector of BC.
Step by step video & image solution for A B C and D B C are two isosceles triangles on the same base B C and vertices A and D are on the same side of BC . If A D is extended to intersect B C at P , show that A B D~=A C D (ii) A B P~=A C P A P bisects /_A as well as /_D A P is perpendicular bisector of B Cdot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD≅ACD (ii) ABP≅ACP AP bisects ∠A as well as ∠D AP is perpendicular bisector of BC.

View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD

View SolutionTriangles ABC and +DBC are on the same base BC with A, D on opposite side of line BC, such that ar(△ABC)=ar(△DBC). Show that BC bisects AD.
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
View SolutionA triangle ABC is an isosceles triangle if any one of the following conditions hold: Altitude AD bisects ∠BAC. Bisector of ∠BAC is perpendicular to the base BC.
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
View Solution