Question

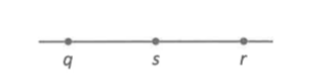
$r>s$
$\begin{array}{cc}\text{Quantity A}& \text{Quantity B}\\ (r+s)(r-s)& (s+r)(s-r)\end{array}$

Options

A. Quantity A is greater.
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the infromation given.

Answer

D

Explanation

To solve the problem, we need to compare the two quantities given the condition $$r>s$$.

1. Understand the Quantities:
- Quantity A: \( (r + s)(r - s) \)
- Quantity B: \( (s + r)(s - r) \)

Since \( s + r = r + s \), we can rewrite Quantity B as:
- Quantity B: \( (r + s)(s - r) \)

2. Rewrite the Quantities:
- Quantity A: \( (r + s)(r - s) \)
- Quantity B: \( (r + s)(s - r) \)

3. Factor Out Common Terms:
Both quantities have a common factor of \( (r + s) \):
- Quantity A: \( (r + s)(r - s) \)
- Quantity B: \( (r + s)(s - r) \)

We can express the comparison as:
\( \text{Compare } (r - s) \text{ and } (s - r) \)

4. Analyze the Factors:
Since \( r > s \), we know:
- \( r - s > 0 \)
- \( s - r < 0 \)

5. Determine the Sign of Each Quantity:
- Quantity A: \( (r + s)(r - s) \) is positive because both \( (r + s) > 0 \) (since both \( r \) and \( s \) are positive) and \( (r - s) > 0 \).
- Quantity B: \( (r + s)(s - r) \) is negative because \( (s - r) < 0 \).

6. Conclusion:
Since Quantity A is positive and Quantity B is negative, we conclude that:
\( \text{Quantity A} > \text{Quantity B} \)

Final Answer:
Quantity A is greater than Quantity B.

---