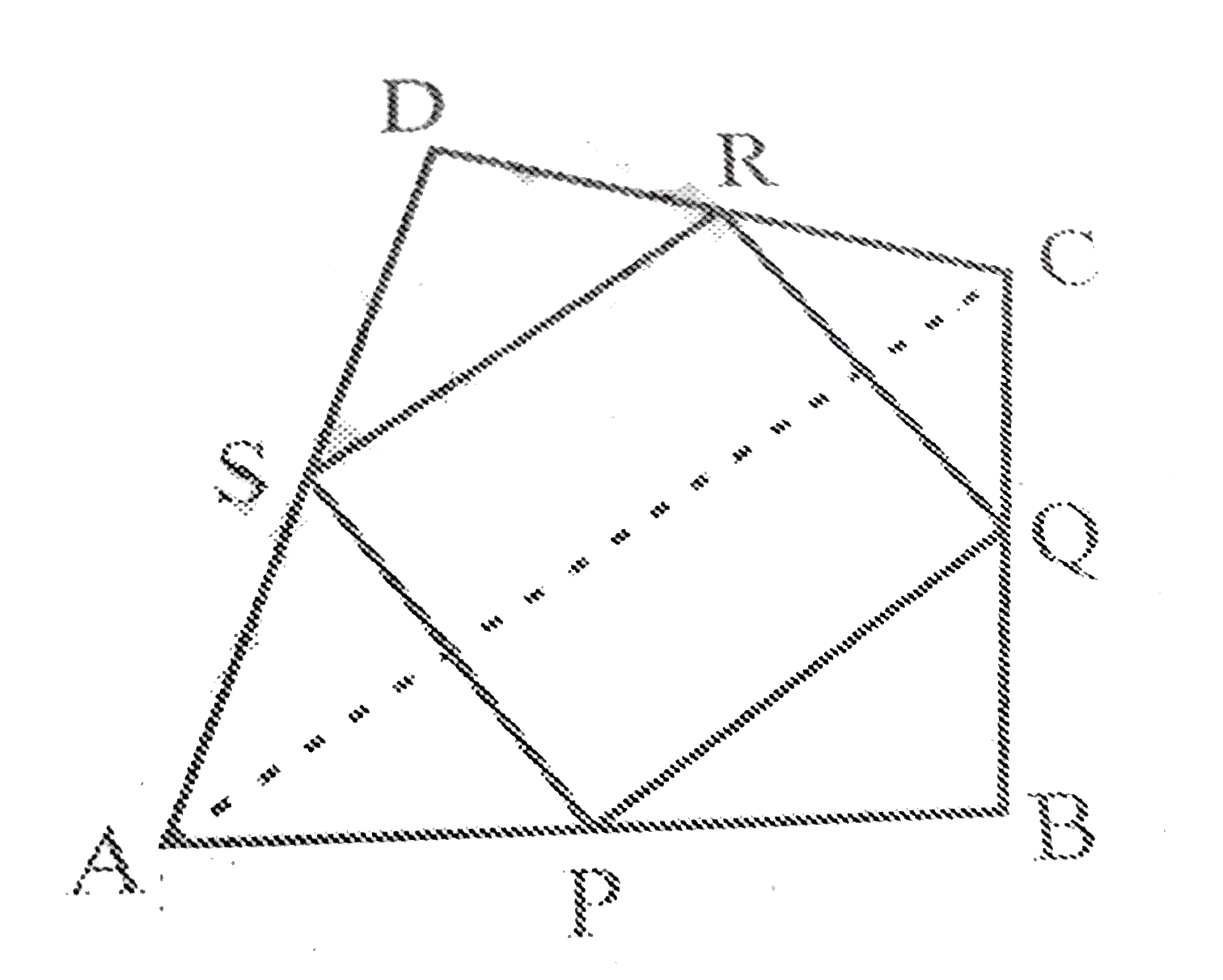
In Figure, PQRS
and ABRS
are parallelograms and X
is any point on side BR.
Show that :
ar(^(gm)PQRS)=ar(^(gm)ABRS)
ar(AXS)=12ar(PQRS)
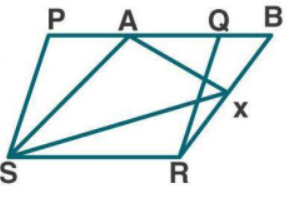
Step by step video & image solution for In Figure, P Q R S and A B R S are parallelograms and X is any point on side B Rdot Show that : a r(^(gm)P Q R S)=a r(^(gm)A B R S) a r(A X S)=1/2a r( P Q R S) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
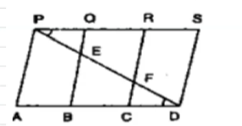
In Figure, PSDA is a parallelogram in which PQ=QR=RS and APBQCR. Prove that ar ( PQE)= ar ( CFD).
View SolutionIn Figure, PQRS is a parallelogram. If XandY are mid-points of PQandSR respectively and diagonal SQ is jointed. The ratio ar(| |(gm)XQRY):ar(QSR)=
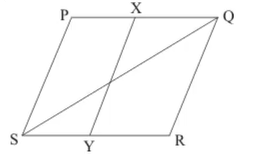
(a) 1:4
(b) 2:1
(c) 1:2
(d) 1:1
View Solution
Knowledge Check
P and Q are brothers, R and S are sister P's son is S's brother. How is Q related to R?
AUncleBBrotherCFatherDGrandfatherWhat should come next in the following letter series ?
P Q P Q R P Q R S P Q R S T P Q R S T L P Q R S T U V P Q R S TASBUCQDR
The side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
View SolutionPQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
(i) SR ∣∣ ACand SR=12AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View Solution
