ABCD is a parallelogram andline segments AX,CY bisect the angles A and C, respectively Figure. Show that AXCY. Figure
Given: ABCD is a parallelogram and line segments AX, CY bisect the angles A and C respectively.
To Prove: AX∣∣CY
Proof: ABCD is a parallelogram
∴∠A=∠C [Opposite ∠s]
12∠A=12∠C [ ∵ Halves of equals are equal]
∠1=∠2 ....(1) [∵AX is the bisector of ∠A and CY is the bisector of ∠C]
Now, AB∣∣DC and CY intersects them
∴∠2=∠3 ...(2) [Alternate interior ∠s]
From (1) and (2), we get:
∠1=∠3
But these form a pair of equal corresponding angles
∴AX∣∣CY
Hence proved.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram andline segments AX,CY bisect the angles A and C, respectively Figure. Show that AXCY. Figure
View SolutionABCD is a parallelogram and line segments AX,CY bisect the angles AandC, respectively. Show that AX∣∣CY
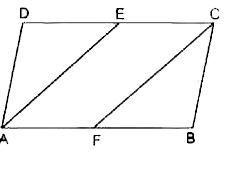
View SolutionIn the adjacent figure , ABCD is a parallelogram and line segments AE and CF bisect the angles A and C respectively . Show that AE∣∣CF.
 View Solution
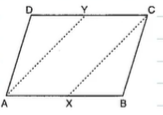
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
 View Solution
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
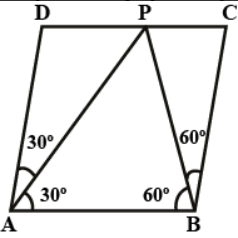
View SolutionIn Figure, ABCD is a parallelogram and ∠DAB=600. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD
 View Solution
View SolutionIn a parallelogram ABCD , write the sum of angle A and B
View SolutionABCD is a parallelogram . If ∠A+∠C=120∘, then ∠B+∠D=________
View SolutionABCD is a parallelogram X and Y are the mid-points of BC and CD respectively. Prove that ar(AXY)=38ar(∣∣gmABCD)
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View Solution

