In the adjacent figure , ABCD is a parallelogram and line segments AE and CF bisect the angles A and C respectively . Show that AE∣∣CF.
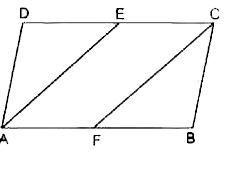
Step by step video & image solution for In the adjacent figure , ABCD is a parallelogram and line segments AE and CF bisect the angles A and C respectively . Show that AE||CF. by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PARALLELOGRAMSBOOK - RS AGGARWALCHAPTER - PARALLELOGRAMSEXERCISE - Exercise 16B
10 Videos
- PARALLELOGRAMSBOOK - RS AGGARWALCHAPTER - PARALLELOGRAMSEXERCISE - Exercise 16B
10 Videos
- OPERATIONS ON ALGEBRAIC EXPRESSIONSBOOK - RS AGGARWALCHAPTER - OPERATIONS ON ALGEBRAIC EXPRESSIONSEXERCISE - Exercise 6E (Tick the correct answer in each of the following:)
19 Videos
- PERCENTAGEBOOK - RS AGGARWALCHAPTER - PERCENTAGEEXERCISE - TEST PAPER -9 ( TRUE AND FALSE )
4 Videos
Similar Questions
Knowledge Check
In the given figure, ABCD is a quadrilateral, the line segments bisecting ∠Cand∠D meet at E. Then 2∠CED is equal to
 A∠A+∠BB∠A+∠CC∠B+∠DD∠C+∠D
A∠A+∠BB∠A+∠CC∠B+∠DD∠C+∠D
ABCD is a parallelogram and AE and CF bisect ∠Aand∠C respectively. Prove that AE||FC.

View SolutionABCD is a parallelogram and bisector of angle A bisects BC at X. Show that AD= 2AB
View SolutionIn the given figure, ABCD is a parallelogram. AE divides the line segment BD in the ratio 1 : 2. If BE = 1.5 cm find BC.

View SolutionThrough the vertex D of a parallelogram ABCD, a line is drawn to intersect the sides BA and BC produced at E and F respectively. Prove that DAAE=FBBE=FCCD
View SolutionIn the adjoining figure, show that ABCD is a parallelogram.
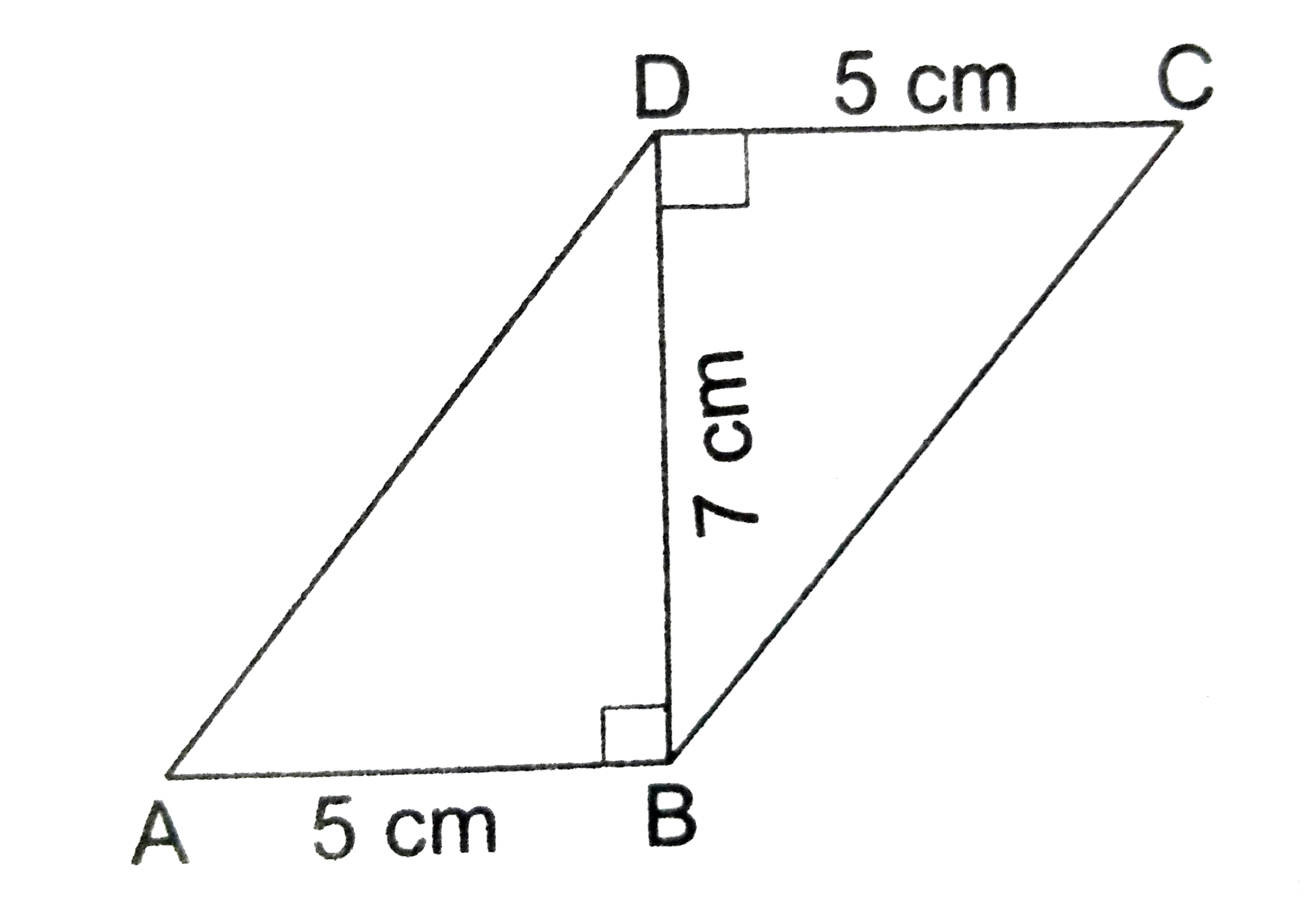
Calculate the area of ||gm ABCD.
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE triset (divide into three equal parts) the diagonal BD.

View SolutionABCD is a parallelogram. ¯¯¯¯¯¯AP bisects ∠Aand¯¯¯¯¯¯CQ bisects ∠C.P lies on ¯¯¯¯¯¯CDandQ lies on ¯¯¯¯¯¯¯¯AB0. Show that -
View Solution
