A point on a string at x=0 has an initial displacement of 12. .If the wave travels to the right, then the corresponding equation is "
Step by step video & image solution for A point on a string at x=0 has an initial displacement of (1)/(2). .If the wave travels to the right, then the corresponding equation is " by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
- A point on a string at x = 0 has an initial displacement A of 2 . If the wave travels to the right, then the corresponding equation is у A A2 X e
View SolutionA series of pulses, each of amplitude 0.150m, are sent on a string that is attached to a wall at one end. The pulses are reflected at the wall and travel back along the string without loss of amplitude. When two waves are present on the same string. The net displacement of a given point is the sum of the displacement of the individuals waves at the point. What is the net displacement at point on the spring where two pulses am crossing, (a) if the string is rigidly attached to the post? (b) if the end at which reflection occurs is free is slide up and down ?
View Solution
Knowledge Check
- Question 1 - Select One
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm will beA3.3cmB6.7cmC4.9cmD2.6cm - Question 2 - Select One
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
If one end of the string is at x=0 , positions of the nodes can be described asAx=nπ/5cm,wheren=0,1,2,…Bx=n2π/5cm,wheren=0,1,2,…Cx=nπ/5cm,wheren=0,1,3,5,…Dx=nπ/10cm,wheren=0,1,3,5,… - Question 3 - Select One
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Figure 7.104( c) shows the standing wave pattern at t=0 due to superposition of waves given by y1 and y2 in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , N is a node and A and antinode . At this instant say t=0 , instantaneous velocity of points on the string
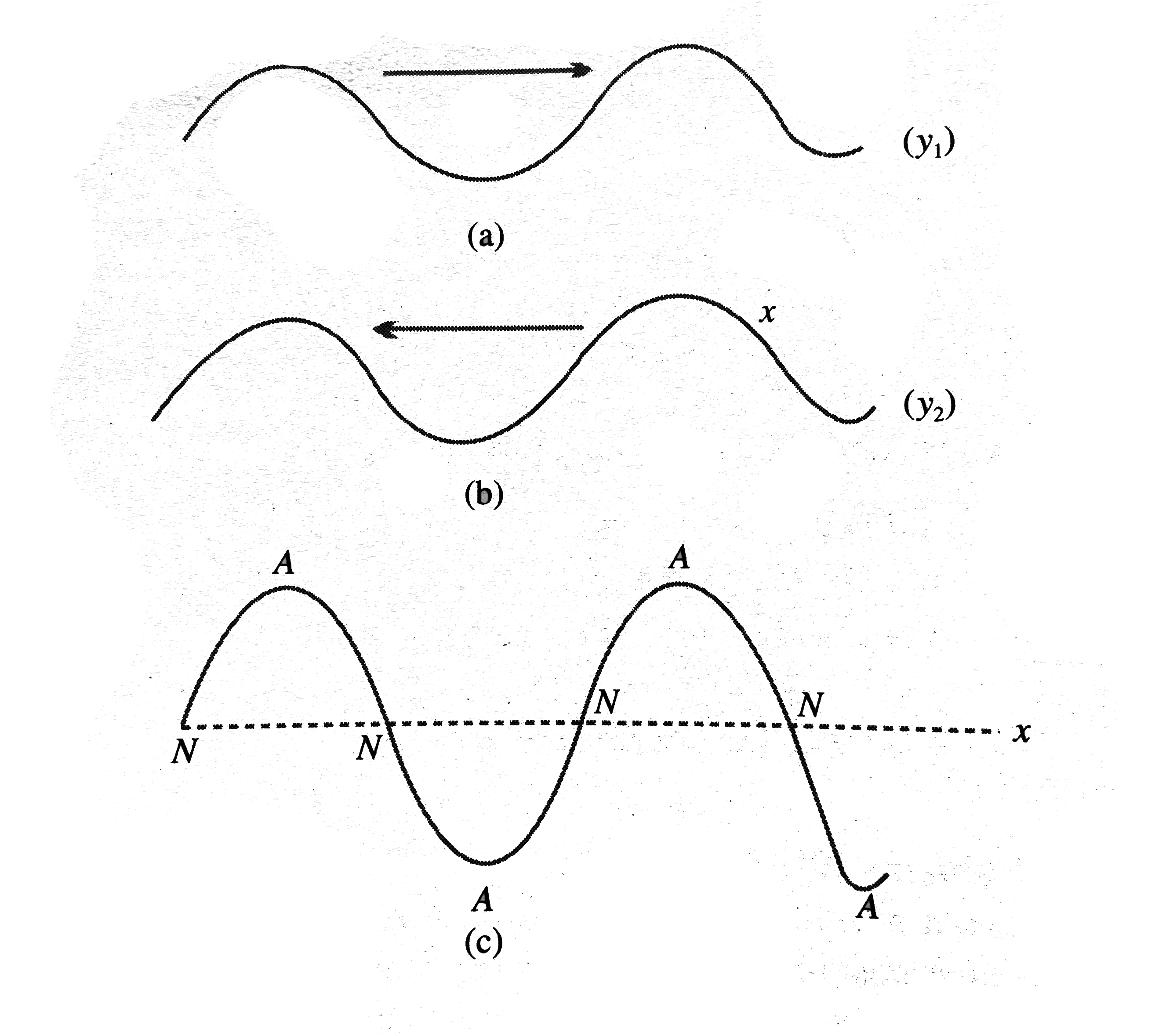 Ais different for different pointsBis zero for all pointsCchanges with position of the pointDis constant but not equal to zero for all points
Ais different for different pointsBis zero for all pointsCchanges with position of the pointDis constant but not equal to zero for all points
A travelling wave is found to have the displacement by y=11+x2 at t = 0, after 3 sec the wave pulse is represented by equation y=11+(1+x)2.The velocity of wave is:
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Maximum value of the y - positions coordinate in the simple harmonic motion of an element of the string that is located at an antinode will beView SolutionA wave in a string has an amplitude of 2cm. The wave travels in the +ve direction of x axis with a speed of 128ms−1 and it is noted that 5 complete waves fit in 4m length of the string. The equation describing the wave is
View Solution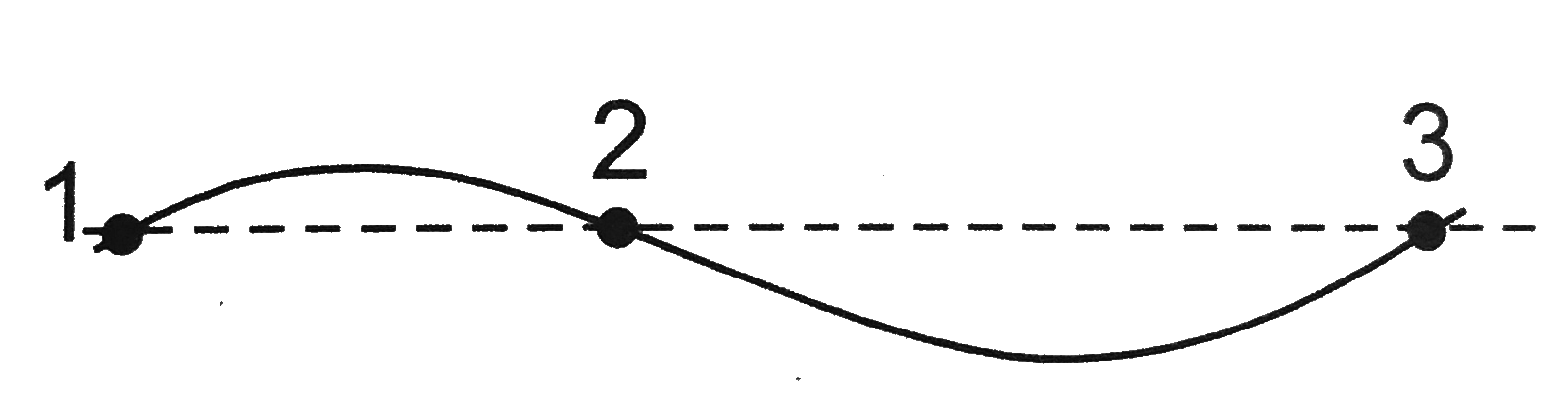
The diagram below shows an instantaneous position of a string as a transverse progressive wave travels along it from left to right Which one of the following correctly shows the direction of the velocity of the points 1,2 and 3 on the string?View SolutionA 200Hz sinusoidal wave is travelling in the positive x-direction along a string with a linear mass density of 3.5×10−3kg/m and a tension of 35N. At time t=0, the point x=0 , has maximum displacement in the positive y-direction. Next when this point has zero displacement, the slope of the string is π/20. Which of the following expression represent (s) the displacement of string as a function of x(in metre) and t (in second)
View Solution
