The angular acceleration of a particle moving along a circle is given by a=ksin (theta),where "theta" is the angle turned by particle and k is constant.The centripetal acceleration of the particle in terms of k ,theta and R (radius of circle) is given by
Step by step video & image solution for The angular acceleration of a particle moving along a circle is given by a=ksin (theta),where "theta" is the angle turned by particle and k is constant.The centripetal acceleration of the particle in terms of k ,theta and R (radius of circle) is given by by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
The kinetic energy K of a particle moving along a circle of radius R depends upon the distance S as K=βS2 , where β is a constant. Tangential acceleration of the particle is proportional to
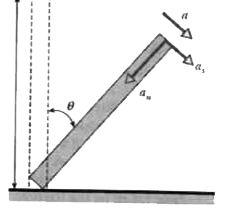
View SolutionThe angular acceleration of the toppling pole shown in fig is given by a=ksinθ, where θ is the angle between the of the pole and the vertical, and k is aconstant. The pole starts from rest at θ=0. Find (a) the tan gential and (b) the centripetal acceleration of the upper end of the pole in terms of k,θ, and (the length of the pole.)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle with the constant speed in a circle of radius r and time period T.The centripetal acceleration of a particle is
A‘r2‘TB‘T2‘rC(2πT)2rD(2πT)2r - Question 2 - Select One
A particle is moving in a circle with a constant speed, the acceleration of the particle has
Aconstant magnitudeBconstant magnitude and directionCboth magnitude and direction changesDneither magnitude nor direction changes - Question 3 - Select One
Centripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
A4 m/rB4m/√rC2m√rD2 m/r
If the equation for the displacement of a particle moving on a circle path is given by, θ=2t2+0.5 where, θ is in radian and t is in second, then the angular velocity of the particle after 2 s is
View SolutionIF the equation for the displancement of a particle moving on a circular path is given by θ=2t3+0.5, where θ is in radius and t is in seconds, then the angular velocity of the particle at t=2 s is
View SolutionThe displacement of a particle moving in a circular path is given by θ=3t2+0.8, where θ is in radian and t is in seconds . The angular velocity of the particle at t=3 sec . Is
View SolutionThe kinetic energy of a particle moving along a circle of radius depends on distance(s) as Kas2, where a is a constant. The centripetal force is given by
View SolutionA particle is moving at uniform speed 2ms−1 along a circle of radius 0.5m.The centripetal acceleration of particle is
View Solution
