The angular acceleration of the toppling pole shown in fig is given by a=ksinθ, where θ is the angle between the of the pole and the vertical, and k is aconstant. The pole starts from rest at θ=0. Find (a) the tan gential and (b) the centripetal acceleration of the upper end of the pole in terms of k,θ, and (the length of the pole.)
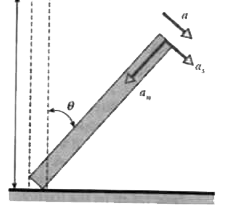
The correct Answer is:(a) lksinθ; (b) 2kl(1−cosθ)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PRACTICE QUESTIONS(SINGLE CORRECT CHOICE TYPE)
40 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PRACTICE QUESTIONS(MORE THAN ONE CORRECT CHOICE TYPE)
6 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - CHECK POINTS
6 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
The angular acceleration of a particle moving along a circle is given by a=ksin (theta),where "theta" is the angle turned by particle and k is constant.The centripetal acceleration of the particle in terms of k ,theta and R (radius of circle) is given by
View SolutionIf cosecθ+cotθ=k then find the value of cosθ in terms of k
View Solution
Knowledge Check
A pole on the ground lenses 60∘ to the vertical. At a point a meters away from the base of the pole on the ground, the two halves of the pole subtend the same angle. If the pole and the point are in the same vertical plane, the length of the pole is
A3aB√3aCa+√33Dnone of theseA pole on the ground leans 60∘ to the vertical. At a point a meters away from the base of the pole on the ground, the two halves of the pole subtend the same angle. If the pole and the point are in the same vertical plane, the length of the pole is
A3aB√3aCa√33Dnone of theseIf the angle of elevation of sun is θ and the length of the shadow of a pole of length p is s, then
Ap=scosθBp=ssinθCp=scotθDp=scotθ
[" The angular acceleration "],[" of a particle moving along "],[" a circle is given by "a=k],[" sin "theta" ,where "theta" is the angle "],[" turned by particle and "k" is "],[" constant.The centripetal "],[" acceleration of the "],[" particle in terms of "k" ,"theta],[" and "R" (radius of circle) is "],[" given by: "]
View SolutionA pole on the ground lenses 60∘ to the vertical. At a point a meters away from the base of the pole on the ground, the two halves of the pole subtend the same angle. If the pole and the point are in the same vertical plane, the length of the pole is
View SolutionA pole on the ground leans at 60° with the vertical. At a point x metre away from the base of the pole on the ground, two halves of the pole subtend the same angle. If the pole and the point are in the same vertical plane, then what is the length of the pole?
View SolutionIf secθ+tanθ=k find the value of cosθ
View SolutionABCD is a square plot . The angle of elevation of the top of a pole standing at D from A and C is 30∘ and that from B is θ, then tanθ is equal to
View Solution
