One end of a massless spring of relaxed length 50cm and spring constant k is fixed on top of a frictionless inclined plane of inclination theta=30degree as shown in fig. When a mass m=1.5kg is attached at the other end, the spring extends by 2.5cm when the block in equilibrium .The mass is displaced slightly from equilibrium position and released. The time period (in seconds) of the resulting oscillation will be (g=9.8m/s^(2))
pi/7
2pi/7
pi/5
2pi/5
The correct Answer is:pi/7
Step by step video & image solution for One end of a massless spring of relaxed length 50cm and spring constant k is fixed on top of a frictionless inclined plane of inclination theta=30degree as shown in fig. When a mass m=1.5kg is attached at the other end, the spring extends by 2.5cm when the block in equilibrium .The mass is displaced slightly from equilibrium position and released. The time period (in seconds) of the resulting oscillation will be (g=9.8m/s^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A spring of unstretched length 40 cm and spring constant k is attached to a block of mass 1 kg to one of its end. The other end of the spring is fixed on the top of a frictionless inclined plane of inclination θ=45∘ as shown in the figure, so that the spring extends by 3 cm. When the mass is displaced slightly and released the time period of the resulting oscillation is T. Determine the value of 5T close to nearest integer.
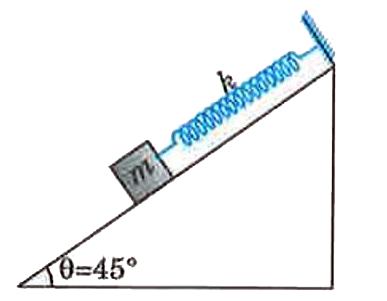 View Solution
View Solution
A 5-kg block rests on a smooth inclined plane of inclination 37∘ as shown in the diagram if the extension of spring is 6cm, find (a) the spring constant (b). If the block is pulled dow the incline 4 cm from its equilibrium position and released, find the initial acceleration of the block.View Solution
Knowledge Check
- Question 1 - Select One
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mK - Question 2 - Select One
Two springs fixed at one end are stretched by 4 cm and 12 cm, respectively, when masses of 0.5 kg and 1 kg are suspended at their lower ends. They are displaced slightly from their mean positions and released. What is the ratio of their periods of oscillation ?
A1:√2B1:2C1:√3D2:5 - Question 3 - Select One or More
A spring of spring constant k stores 5 J of energy when stretched by 25 cm. It is kept vertical with one end fixed. A mass m is attached to the other end. It maskes 5 Oscillation per second. Then
Am=0.16kgBm=0.32kgCk=160NmDk=320Nm
A horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
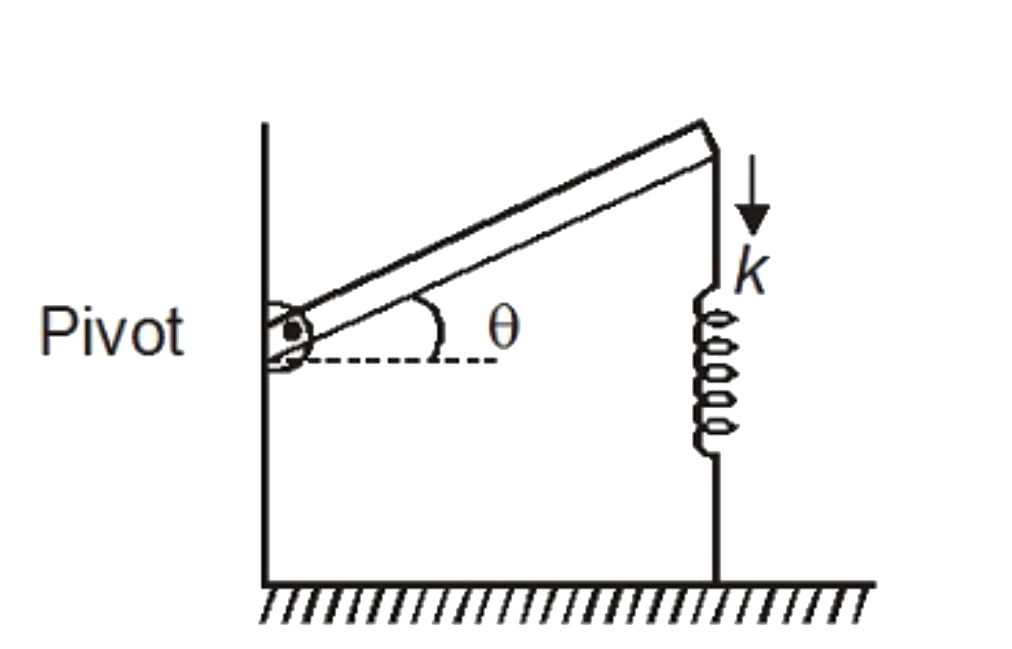 View Solution
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
 View Solution
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.
 View Solution
View SolutionTwo identical springs are attached to a small block P. The other ends of the springs are fixed at A and B, When P is in equilibrium the extension of bottom spring is 10 cm. The period of small vertical oscillations of P about is equilibrium position is (useg=9.8m/s2)
 View Solution
View Solution
