For a reaction of the type Aa+bB→products
(−)d[A]dt is equal to
(A) −d[B]dt
(B) −bdd[B]dt
(C) −ab×d[B]dt
(D) −ba×d[B]dt
Step by step video & image solution for For a reaction of the type Aa+bB rarr products ( -)(d[A])/(dt) is equal to (A) (-d[B])/(dt) (B) -(b)/(d)(d[B])/(dt) (C) -(a)/(b)times(d[B])/(dt) (D) -(b)/(a)times(d[B])/(dt) by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
For the reaction 2A+B to product , (d[A])/(dt)=K[A]^(2)[B] . What will be rate equation for -(d[B])/(dt) ?
View SolutionFor a reaction, 2A+BtoC+D,(d[A])/dt=K[A]^2[B] The expression for (d[B])/dt will be:
View SolutionFor a reaction, 2A+BtoC+D,(d[A])/dt=K[A]^2[B] The expression for (d[B])/dt will be:
View SolutionMechanism of the reaction is: What is (a) (-d[A])/(dt) , (b) (d[A_(1)])/(dt)
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
For reaction 3BrOɵ→BrOɵ3+2Brɵ, the value of rate constant at 80∘C in the rate law for −d[BrOɵ]dt was found to be 0.054Lmol−1s−1. The rate constant (k) for the reaction in terms of d[BrOɵ3]dt is
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
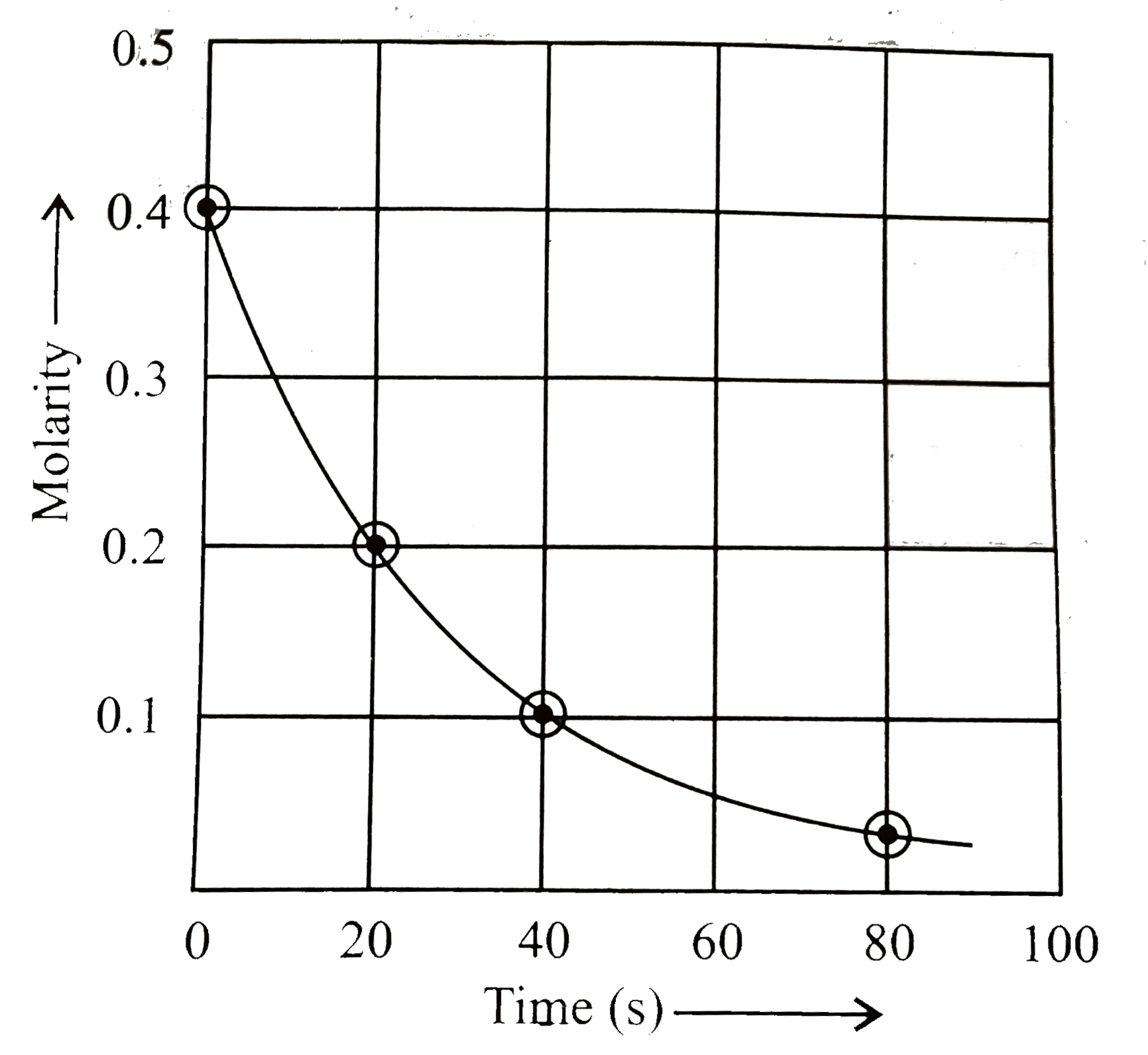
A reaction follows the given concentration-time graph. The rate for this reaction at 20s will be
View SolutionFor the reaction: aA + bB rarr cC+dD Rate = (dx)/(dt) = (-1)/(a)(d[A])/(dt) = (-1)/(b)(d[B])/(dt) = (1)/( c)(d[C])/(dt) = (1)/(d)(d[D])/(dt) In the following reaction, xA rarr yB log.[-(d[A])/(dt)] = log.[(d[B])/(dt)] + 0.3 where negative isgn indicates rate of disappearance of the reactant. Thus, x:y is:
View Solution