For the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
For reaction 3BrOɵ→BrOɵ3+2Brɵ, the value of rate constant at 80∘C in the rate law for −d[BrOɵ]dt was found to be 0.054Lmol−1s−1. The rate constant (k) for the reaction in terms of d[BrOɵ3]dt is
0.018Lmol−1s−1
0.162Lmol−1s−1
0.036Lmol−1s−1
None of these
The correct Answer is:A
To find the rate constant k for the reaction 3BrO∘→BrO∘3+2Br∘ in terms of d(BrO∘3)dt, we can follow these steps:
Step 1: Write the rate expressions for the reaction
For the reaction 3BrO∘→BrO∘3+2Br∘, the rate can be expressed in terms of the change in concentration of each species:
−13d(BrO∘)dt=11d(BrO∘3)dt=12d(Br∘)dt
Step 2: Relate the rates to the rate constant
From the rate expression, we know that the rate of the reaction can be expressed in terms of the rate constant k and the concentration of the reactants. For the rate law of −d(BrO∘)dt:
−d(BrO∘)dt=k(BrO∘)3
Step 3: Express the rate in terms of d(BrO∘3)dt
From the rate expressions, we can express the rate of formation of BrO∘3 in terms of the rate of consumption of BrO∘:
d(BrO∘3)dt=−13d(BrO∘)dt
Step 4: Substitute the known rate constant
Given that the rate constant k for the reaction in terms of −d(BrO∘)dt is 0.054L mol−1s−1, we can express the rate constant for d(BrO∘3)dt:
k′=13k
Step 5: Calculate the new rate constant
Substituting the value of k:
k′=13×0.054L mol−1s−1=0.018L mol−1s−1
Final Answer
Thus, the rate constant k′ for the reaction in terms of d(BrO∘3)dt is:
0.018L mol−1s−1
For the reaction 3BrO∘→BrO∘3+2Br∘, the rate can be expressed in terms of the change in concentration of each species:
From the rate expression, we know that the rate of the reaction can be expressed in terms of the rate constant k and the concentration of the reactants. For the rate law of −d(BrO∘)dt:
From the rate expressions, we can express the rate of formation of BrO∘3 in terms of the rate of consumption of BrO∘:
Given that the rate constant k for the reaction in terms of −d(BrO∘)dt is 0.054L mol−1s−1, we can express the rate constant for d(BrO∘3)dt:
Substituting the value of k:
Thus, the rate constant k′ for the reaction in terms of d(BrO∘3)dt is:
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Multiple Correct
33 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Single Correct
177 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex4.4 Objective
10 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
For the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
A reaction follows the given concentration-time graph. The rate for this reaction at 20s will be
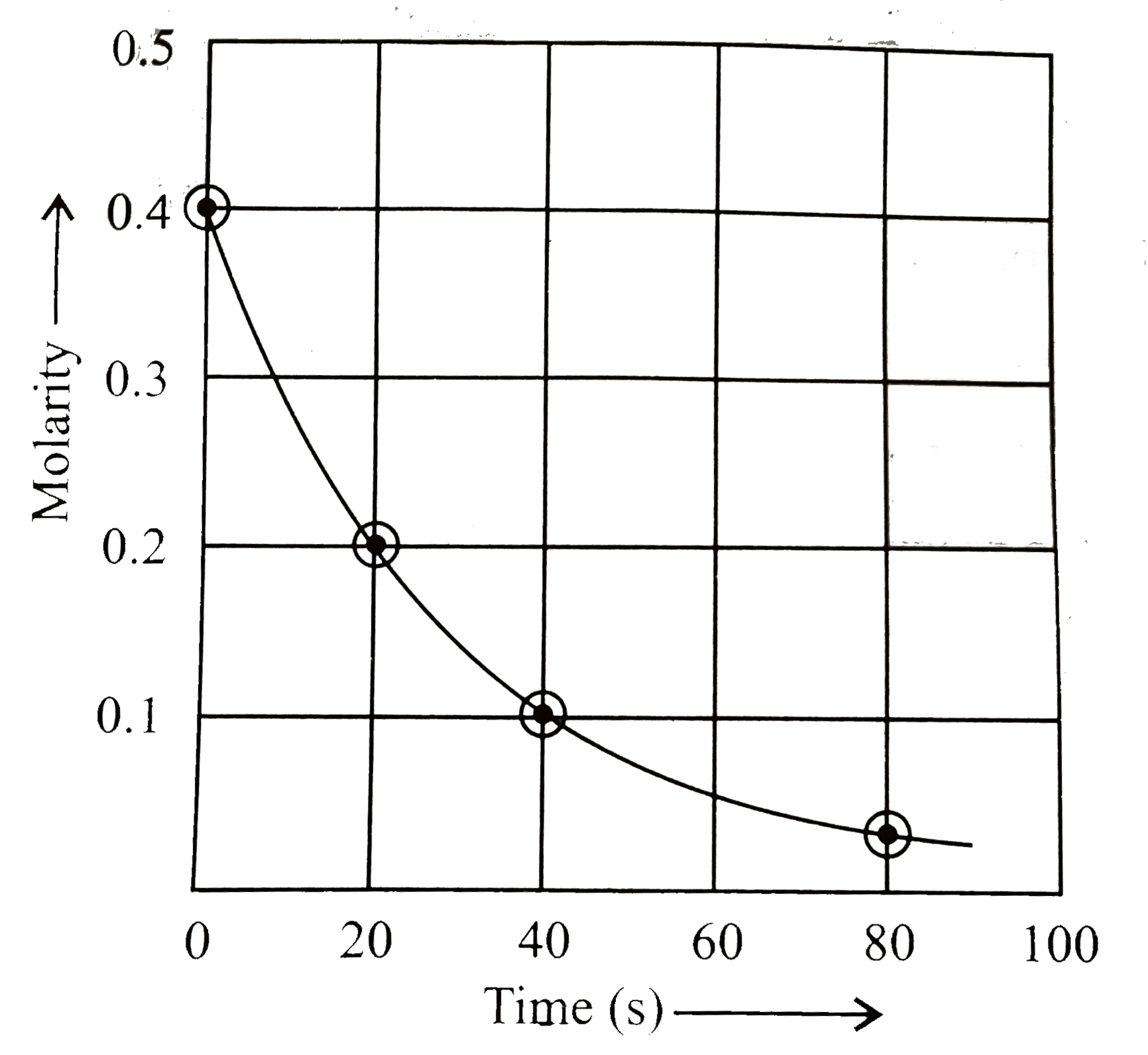
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
The rate of formation of SO3 in the following reaction 2SO2+O2→2SO3 is 100g−1min. Hence the rate of disappearance of O2 is
View SolutionFor the reaction: aA+bB→cC+dD
Rate =dxdt=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt
In the following reaction,
xA→yB
log.[−d[A]dt]=log.[d[B]dt]+0.3
where negative isgn indicates rate of disappearance of the reactant. Thus, x:y is:
View SolutionThe rate of a reaction is expressed in different ways as follows:
+12d[C]dt=−12d[D]dt=+13d[A]dt=−d[B]dt
the reaction is
View SolutionThe rate of a reaction is expressed in different ways as follows:
+12d[C]dt=−13d[D]dt=+14d[A]dt=−d[B]dt
the reaction is
View SolutionIn a reaction,
aA+bB→cC+dD
rate =−1ad[A]dt , the - ve sign in it represents
View SolutionFor the reaction 2A→B+3C, if −d[A]dt=k1[A]2,−d[B]dt=k2[A]2,−d[C]dt=k3[A]2 the correct reaction between k1,k2 and k3 is :
View SolutionMechanism of the reaction is:
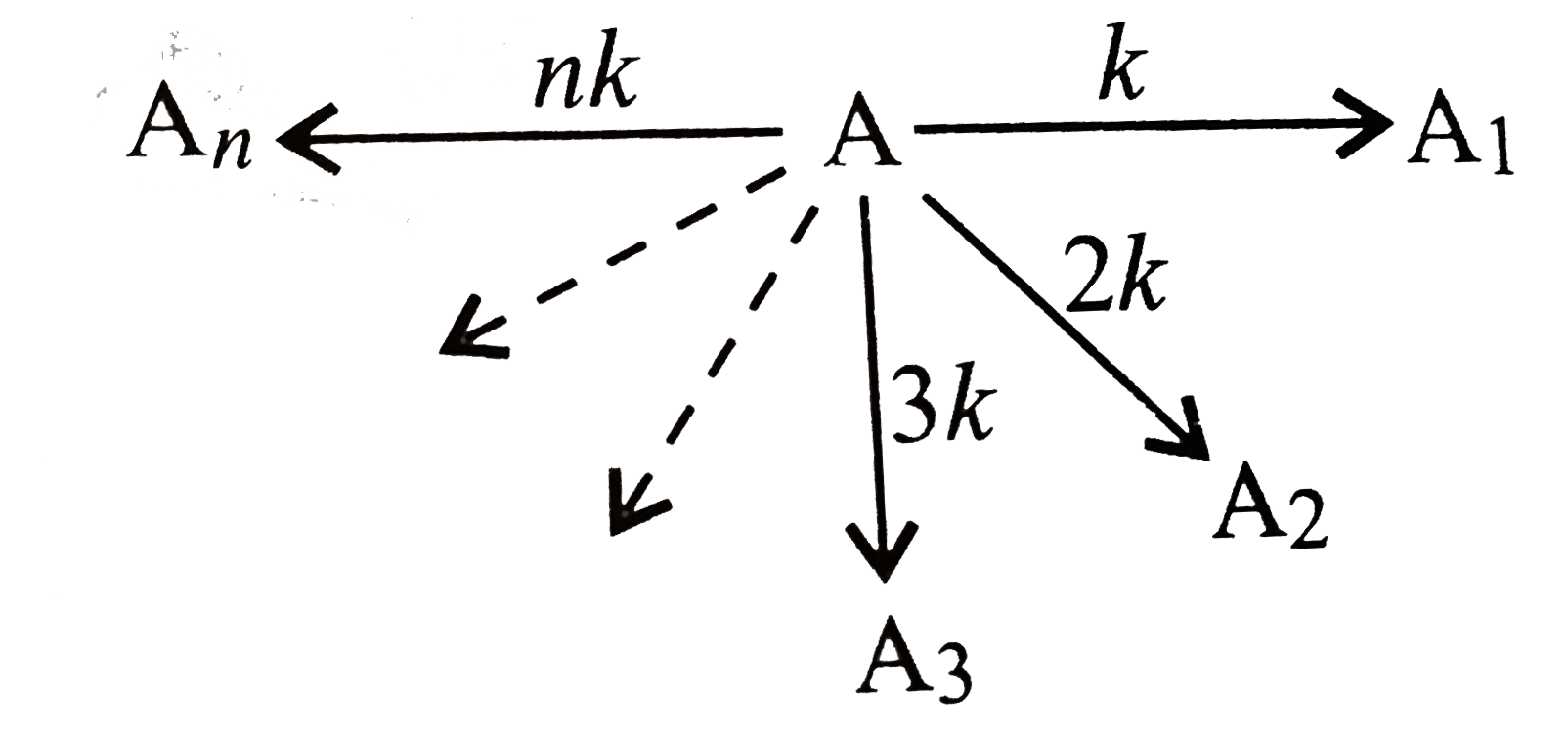
What is (a) −d[A]dt, (b) d[A1]dt
View SolutionIn the reaction 3A→2B, rate of reaction +d[B]dt is equal to :
View SolutionA+2B→C+D. If −d[A]dt=5×10−4 mol L−1s−1, then −d[B]dt is :
View Solution
