The straight line x + 2y = 1 meets the coordinate axes at A and B. A circle is drawn through A,B and the origin. Then, the sum of perpendicular distances from A and B on the tangent to the circle at the origin is
2√5
√54
4√5
√52
The correct Answer is:D
According to given information, we have the following figure.
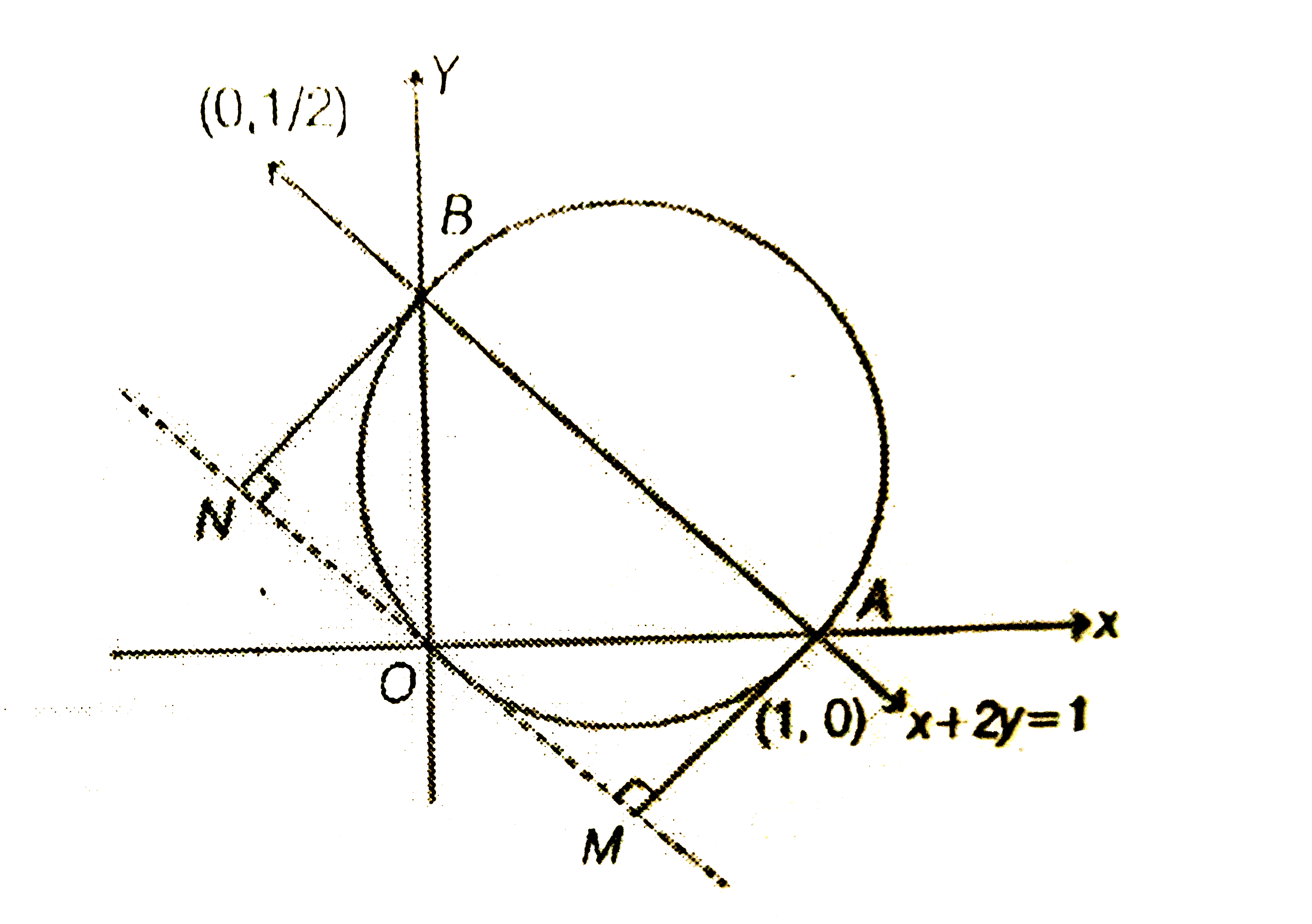
From figure, equation of circle (diameter form) is
(x−1)(x−0)+(y−0)((y−12)=0
⇒x2+y2−x−y2=0
Equation of tangent at (0, 0) is x+(y)+(2)=0
[∴ equation of tangent at (x1,y1) is given by T=0 Here ,T=0
⇒xx1+yy1−12(x+x1)−14(y+y1)=0]
⇒2x+y=0
Now, AM=|2.1+1.0|√5=2√5
[∴ distance of a point P(x1,y1) from a line
ax+by+c=0 is |ax1+by1+c|√a2+b2]
and BN=∣∣2.0+1(12)∣∣√5=12√5
∴AM+BN=2√5+12√5=4+12√5=√52
Topper's Solved these Questions
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 3 Objective Question II
Explore 2 Videos
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 3 Assertion and Reason
Explore 1 Video
- CIRCLEBook:IIT JEE PREVIOUS YEARChapter:CIRCLEExercise:Topic 2 Analytical & Descriptive Questions
Explore 2 Videos
- BINOMIAL THEOREMBook:IIT JEE PREVIOUS YEARChapter:BINOMIAL THEOREMExercise:Topic 2 Properties of Binomial Coefficent Objective Questions I (Only one correct option) (Analytical & Descriptive Questions )
Explore 8 Videos
- COMPLEX NUMBERSBook:IIT JEE PREVIOUS YEARChapter:COMPLEX NUMBERSExercise:TOPIC 5 DE-MOIVRES THEOREM,CUBE ROOTS AND nth ROOTS OF UNITY (INTEGER ANSWER TYPE QUESTION)
Explore 1 Video
Similar Questions
A line 2x+y=1 intersect co-ordinate axis at points A and B. A circle is drawn passing through origin and point A & B. If perpendicular from point A and B are drawn on tangent to the circle at origin then sum of perpendicular distance is (A) 5√2 (B) √52 (C) √54 (D) 52
View SolutionA line 2x+y=1 intersect co-ordinate axis at points A and B. A circle is drawn passing through origin and point A & B. If perpendicular from point A and B are drawn on tangent to the circle at origin then sum of perpendicular distance is (A) 5√2 (B) √52 (C) √54 (D) 52
View Solution
Knowledge Check
A straight line x+2y=1 cuts the x and y axis at A and B.A circle passes through point A and B and origin.Then the sum of length of perpendicular from A and B on tangent of the circle at the origin is
A√54B√53C√52D√5A line meets the coordinate axes at A and B. A circle is circumscribed obout the triangle OAB. If the distance of the points A and B from the tangent at O, the origin, to the circle are m and n respectively, find the diameter of the circle.
A2m+n2B(m+n)Cmnm+nDm+2n2A line meets the co-ordinates axes at A(a, 0) and B(0, b) A circle is circumscribed about the triangle OAB. If the distance of the points A and B from the tangent at origin to the circle are 3 and 4 repectively, then the value of a2+b2+1 is
A20B30C40D50
The straight line xa+yb=1 cuts the coordinate axes at A and B . Find the equation of the circle passing through O(0,0),AandB.
View SolutionA line meets the co-ordinates axes at A(a, 0) and B(0, b) A circle is circumscribed about the triangle OAB. If the distance of the points A and B from the tangent at origin to the circle are 3 and 4 repectively, then the value of a2+b2+1 is
View SolutionA circle with center (a,b) passes through the origin. The equation of the tangent to the circle at the origin is ax−by=0 (b) ax+by=0 bx−ay=0 (d) bx+ay=0
View SolutionA parabola y=ax2+bx+c(ac>0) crosses the x-axis at A and B. A variable circle is drawn passing through A and B. The length of a tangent from the origin to the circle is
View SolutionA line makes equal intercepts of length a on the coordinate axes. A circle is circumscribed about the triangle which the line makes with the coordinate axes. The sum of the distance of the vertices of the triangle from the tangent to this circle at the origin is
View Solution
