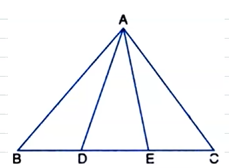
A point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
Proof:
In△ABC,BD=2DC
Let E be the mid point of BD.
∴BE=ED=DC
SinceAE and AD are medians of △ABD and △AEC respectively
∴ar(ABD)=2ar(AED) and ar(ADC)=ar(AED)
⇒ar(ABD)=2ar(ADC)
Hence Proved.
Topper's Solved these Questions
Similar Questions
A point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View SolutionA point D is taken on the side BC of a ABC such that BD=2DC. Prove that ar ( ABD)= 2 ar ( ADC)
View SolutionIn Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
 View Solution
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(EBG)=ar(EFC)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: ar(EFC)=12ar(EBF)
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).
 View Solution
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that : ar(ADEG)=ar(GBCE) ar(EGB)=16ar(ABCD)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(ADEG)=ar(GBCE)
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LBC)=ar(MBC)View Solution

