The balancing length for a cell in a potentiometer experiment is 45 cm. In the balanced condition, the current through the potentiometer wire is 2 A. If the total length of the potentiometer wire is 1 m and its total resistance is60Ω , the emf of the cell is (in Volts) _________.
To solve the problem, we will follow these steps:
Step 1: Calculate the total potential drop across the potentiometer wire
The total resistance of the potentiometer wire is given as R=60Ω and the current flowing through it is I=2A. The potential drop V across the potentiometer wire can be calculated using Ohm's Law:
V=I×R
Substituting the given values:
V=2A×60Ω=120V
Step 2: Calculate the potential gradient (potential drop per unit length)
The total length of the potentiometer wire is L=1m=100cm. The potential gradient k can be calculated by dividing the total potential drop by the total length of the wire:
k=VL=120V100cm=1.2V/cm
Step 3: Calculate the EMF of the cell using the balancing length
The balancing length l is given as 45cm. The EMF E of the cell can be calculated by multiplying the potential gradient k by the balancing length l:
E=k×l=1.2V/cm×45cm
Calculating this gives:
E=54V
Final Answer
The EMF of the cell is 54V.
---
The total resistance of the potentiometer wire is given as R=60Ω and the current flowing through it is I=2A. The potential drop V across the potentiometer wire can be calculated using Ohm's Law:
The total length of the potentiometer wire is L=1m=100cm. The potential gradient k can be calculated by dividing the total potential drop by the total length of the wire:
The balancing length l is given as 45cm. The EMF E of the cell can be calculated by multiplying the potential gradient k by the balancing length l:
The EMF of the cell is 54V.
Similar Questions
When a balance point is obtained in a potentiometer for finding the internal resistance of a cell, the current through the potentiometer wire is due to
View SolutionA cell is balanced at 100cm of a potentiometer wire when the total length of the wire is 400cm .If the length of the potentiometer wire is increased by 100cm ,then the new balancing length for the cell will be
View Solution
Knowledge Check
A Leclanche cell of emf 1.46 V balances against 292 cm of a potentio meter wire. If the current through the wire is 400 mA, the resistance per unit length of the potentiometer wire is
A2Ω/mB2Ω/cmC12.5Ω/mD12.5Ω/cmIn comparing emf's of 2 cells with the helf of potentiometer, at the balance point, the current flowing through the wire is taken from
Aany one of these cells.Bboth of these cellsCbettery in the primary circuitDfrom an unknown sourceIn potentiometer experiment, null point isobtained at a particular point for a cell on potentiometer wire x cm long. If the lengthof the potentiometer wire is increasedwithout changing the cell, the balancing length will (Driving source is not changed)
AincreaseBdecreaseCnot changeDbecome zero
Calculate the value of unknown potential V for the given potentiometer circuit .The total length 400cm of potentiometer wire has a resistance of 10Ω and the balance point in obtained at a length of 240cm
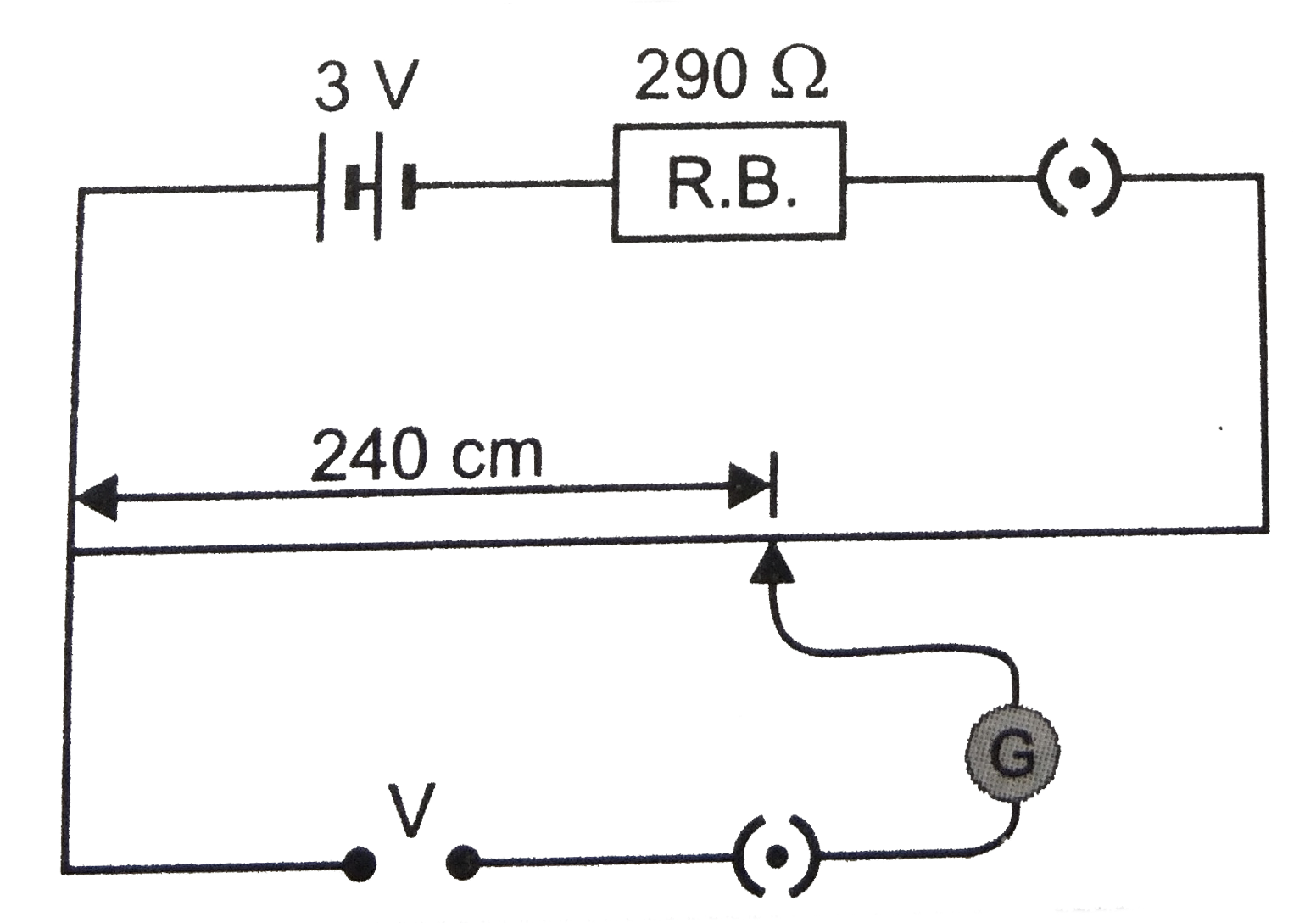
View SolutionA constant voltage of 3 V is supplied to a potentiometer wire. A cell of emf 2 V is balanced by a voltage drop across 416 cm of the wire. Find the total length of the potentiometer wire.
View SolutionIt is observed in a potentiometer experiment that no current passes through the galvanometer, when the terminals of the potentiometer, wire. On shunting the cell by a 2Ω resistance, the balancing length is reduced to half. The internal resistance of the cell is:-
View SolutionIn an experiment to find the internal resistance of a cell by a potentiometer, a balance was obtained for 50 cm length of the potentiometer wire, with a cell of e.m.f. 2V. When the cell was shunted by a resistance of 2Ω, the balancing length of the potentiometer wire was 40 cm. What was the internal resistance of the cell ?
View SolutionIn a potentiometer experiment the balancing with a cell is at length 240 cm. On shunting the cell with a resistance of 2Ω, the balancing length becomes 120 cm.The internal resistance of the cell is
View Solution
